а=2/9 pi
Наименьший положительный корень.
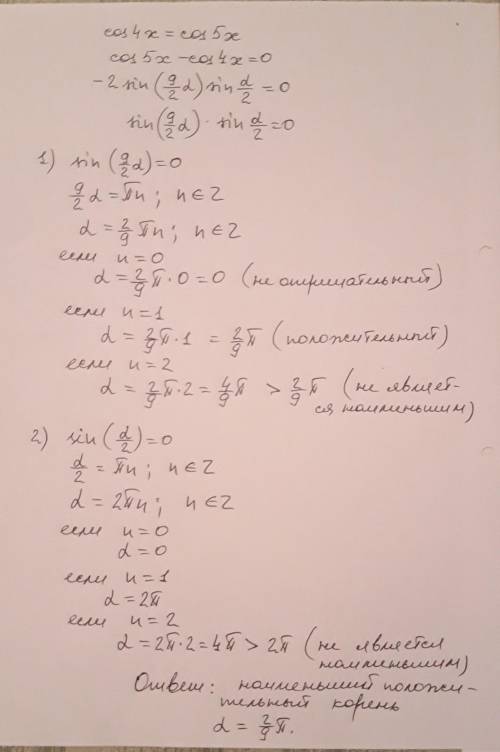
6/Задание № 5:
Сливы разложили на 5 тарелок поровну. Аня съела все сливы с одной тарелки, затем половину слив с другой тарелки и ещё треть слив с третьей тарелки, на тарелках осталось всего 19 слив. Сколько слив съела Аня?
РЕШЕНИЕ: Найдем сколько "тарелок" съела Аня: 1+1/2+1/3=6/6+3/6+2/6=11/6. Значит, осталось в наличии 5-11/6=30/6-11/6=19/6 "тарелок". Эта величина соответствует 19 сливам. Так как количество тарелок пропорционально количеству слив, составляем пропорцию:
(11/6)/(19/6)=х/19, где х -число съеденных слив
11/19=х/19
х=11
ОТВЕТ: 11 слив
Сторона квадрата равна 8 см.
Пошаговое объяснение:
Обозначения:
a -- сторона равностороннего треугольника
b -- сторона квадрата
Pтр -- периметр равностороннего треугольника
Pкв -- периметр квадрата
Дано:
a = b – 3 (сторона равностороннего треугольника на 3 см меньше, чем сторона квадрата)
Pкв = Pтр + 17 (периметр квадрата на 17 см больше, чем периметр равностороннего треугольника)
Найти: b (сторону квадрата).
Периметр треугольника равен Pтр = 3a, периметр квадрата равен Pкв = 4b. Подставим эти выражения в условие Pкв = Pтр + 17:
4b = 3a + 17
Подставим выражение a = b – 3 из условия задачи в получившееся уравнение и решим его относительно неизвестного b:
4b = 3(b – 3) + 17
4b = 3b – 9 + 17
4b – 3b = 17 – 9
b = 8 см -- искомая сторона квадрата
Проверка:
Если сторона квадрата равна 8 см, то его периметр составляет 8·4 = 32 см. Сторона треугольника на 3 см меньше стороны квадрата, то есть 5 см, а периметр треугольника равен 5·3 = 15 см. Разница составляет 32 – 15 = 17 см, т.е. периметр квадрата в самом деле на 17 см больше периметра треугольника.
Решение задания прилагаю. Второй Да, 2рi/9.