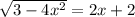
Пошаговое объяснение:
√(3-4x²)=2x+2, где 3-4x²≥0; (2x)²≤3; x₁≥-(√3)/2; x₂≤(√3)/2; -(√3)/2≤x≤(√3)/2
3-4x²=(2x+2)²
3-4x²=4x²+8x+4
4x²+8x+4-3+4x²=0
8x²+8x+1=0; D=64-32=32
x₁=(-8-4√2)/16=(-2-√2)/4; -(2√3)/4<(-2-√2)/4<(2√3)/4
x₂=(-8+4√2)/16=(√2 -2)/4; -(2√3)/4<(√2 -2)/4<(2√3)/4
ответ: (-2-√2)/4 и (√2 -2)/4.
Сумма корней:
(-2-√2)/4 +(√2 -2)/4=(-2-√2 +√2 -2)/4=-4/4=-1
Если даны промежутки, тогда сам уже определишь.
I. (2sin²x - 7sinx + 3) · log₂ (x-8) = 0
ОДЗ : x-8 > 0; x > 8
Произведение равно нулю, когда один из множителей равен нулю.
1) 2sin²x - 7sinx + 3 = 0 - квадратное уравнение с неизвестным sinx
D = 7² - 4·2·3 = 25 = 5²
sin x = (7+5)/4 = 3 - не подходит под условие |sin x| ≤ 1
sin x = (7-5)/4 = 1/2
x₁ = π/6 + 2πn, n∈N, n≥2 ( ОДЗ: π/6 + 4π ≈ 13,1 > 8)
x₂ = 5π/6 + 2πk, k∈N ( ОДЗ: 5π/6 + 2π ≈ 8,9 > 8)
2) log₂ (x-8) = 0 ⇒ x - 8 = 2⁰
x = 1 + 8; x₃ = 9
==========================
II. x ∈ (3π; 6π)

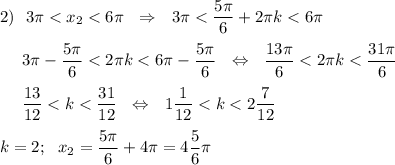
3) x₃ = 9 < 9,4 ≈ 3π - не входит в интервал
ответ:  ;
; 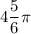
ответ: ряд сходится, при решении задачи использован признак сравнения.
Пошаговое объяснение:
Сравним это ряд с рядом обратных квадратов ∑1/n², который, как известно, сходится. Для этого составим разность 1/n²-(n+1)/(n⁴+1)=(n⁴-n³-n²+1)/[n²*(n⁴+1)]. Так как знаменатель этой дроби положителен при любом n, то её знак будет зависеть от знака числителя n⁴-n³-n²+1. Но n⁴-n³-n²+1=n²*[(n-1/2)²-5/4]+1=n²*(n-1/2)²-5/4*n²+1. Отсюда следует, что числитель обращается в ноль лишь при n=1; если же n>1, то он положителен, а это значит, что при n>1 1/n²>(n+1)/(n⁴+1). Поэтому данный ряд сходится.
√(3 - 4x²) = 2x + 2
ОДЗ 3 - 4x² >= 0 -√3/2 <= x <= √3/2
2x + 2 >= 0 x >= -1
x ∈ [-√3/2, √3/2]
обе части положительны - возводим в квадрат
3 - 4x² = (2x + 2)²
3 - 4x² = 4x² + 8x + 4
8x² + 8x + 1 = 0
D = b² - 4ac = 8² - 4*8*1 = 64 - 32 = 32
x12 = (-8 +- √32)/16 = (-8 +- 4√2)/16 = (-2 +- √2)/4
x1 = (-2 - √2)/4 > -√3/2
-√3/2 ≈ -0.86
(-2 - √2) / 4 ≈ - 0.85
x2 = (-2 + √2 )/4 > -√3/2
x1 + x2 = (-2 - √2)/4 + (-2 + √2)/4 = -4/4 = -1
промежуток, который включает -1