Question

Решиет чрез дискриминат х²+10х+21=0 у²+11у+24=0

Answer 1

1.  x² + 10x + 21 = 0

Найдем дискриминант квадратного уравнения:

D = b² - 4ac = 10²- 4·1·21 = 100 - 84 = 16

Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:

x₁ =  

x₂ =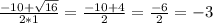 $\frac{-10+\sqrt{16} }{2*1} =\frac{-10+4}{2} =\frac{-6}{2} =-3$

ответ: х₁= -7; х₂= -3

2.   y² + 11y+ 24 = 0

Найдем дискриминант квадратного уравнения:

D = b² - 4ac = 11² - 4·1·24 = 121 - 96 = 25

Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:

y₁ =  

y₂ =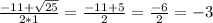  $\frac{-11+\sqrt{25} }{2*1} =\frac{-11+5}{2} =\frac{-6}{2} =-3$

ответ: y₁= -8; y₂= -3.

Answer 2

Здравствуйте!

№1 x=-7 и х=-3 №2 y=-8 и y=-3

Пошаговое объяснение:

№1

$\dispaystyle x^{2} +10x+21=0\\D=b^{2} -4ac=10^{2}-4*21*1=100-84=16 \:\:\: \: \: \: \: \sqrt{D} =4\\\\x_{1}=\frac{-b-\sqrt{D} }{2a} =\frac{-10-4}{2} =-7\\\\x_{2}=\frac{-b+\sqrt{D} }{2a} =\frac{-10+4}{2} =-3\\$

№2

$y^{2}+11y+24=0\\D=b^{2} -4ac=11^{2} -4*24*1=121-96=25 \:\:\:\:\:\:\:\: \sqrt{D}=5\\\\y_{1}=\frac{-b-\sqrt{D} }{2a} =\frac{-11-5}{2} =-8\\\\ y_{2}=\frac{-b+\sqrt{D} }{2a} =\frac{-11+5}{2} =-3$