1)|9-x|<2,если x>_0
9-x<2
-x<2-9 |*(-1)
x<7
(-бесконечность;7)
|9-x|<2,если x<0
9+x<2
x<2-9
x<-7
(-бесконечность;-7)
ответ:(-бесконечность:-7);(-бесконечность;7)
2)|x+7|>8,если x>_0
x+7>8
x>8-7
x>1
(1;+бесконечность)
|x+7|>8,если x<0
x-7>8
x>8+7
x>15
(15;+бесконечность)
ответ:(1;+бесконечность);(15;+бесконечность)
3)|10+x|_<3,если x>_0
10+x_<3
x_<3-10
x_<-7
(-бесконечность;7]
|10+x|_<3,если x<0
10-x_<3
-x_<3-10 |*(-1)
x >_7
[7;+бесконечность)
ответ:(-бесконечность;7];[7;+ бесконечность)
4)|x-8|_>9,если x>_0
x-8_>9
x_>9+8
x_>16
[16;+бесконечность)
|x-8|_>9,если x<0
x+8_>9
x_>9-8
x_>1
[1;+ бесконечность)
ответ:[1;+бесконечность);[16;+бесконечность)
Пошаговое объяснение:
Могу ответь только на 4 прости
1).Х=6; Х=2.
2). У=-2 или У=-8;
3). Х=-1,5 или Х=1,5
4). Пустое множество
5) х=2 или Х=-8
6) пустое множество
Пошаговое объяснение:
1). |Х-4|=2;
Х-4=2 или Х-4=-2 тогда
Х=2+4 или Х=-2+4 и
Х=6 либо Х=2
2) |y+5|=3;
У+5=3 или У+5=-3;
У=3-5 или У=-3-5;
У=-2 или У=-8;
3). |3+x|=1,5;
3+х=1,5 или 3+х=-1,5;
Х=1,5-3 или Х= -1,5+3
Х=-1,5 или Х=1,5
4). |7-y|=-2; модуль выражения либо числа не может быть отрицательным числом
5) |x+3|+4=9;
|х+3|=9-4= 5;
Х+3=5 или Х+3 =-5
Х=5-3=2 или Х=-5-3=-8
6). |y-2|+8=5.
|У-2|= 5-8=-3 - модуль не может быть отрицательным число
просто так
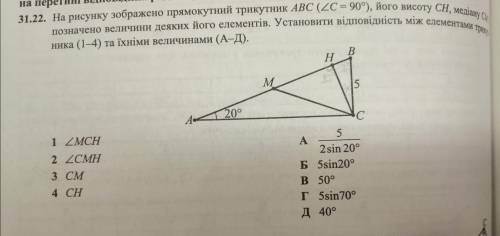
1 ∠MCH → В 50°
2 ∠CMH → Д 40°
3 СМ → А 5/2sin20°
4 CH → Г 5sin70°
Пошаговое объяснение: ∠B=90° -∠A=90° -20°=70°
CM = AB/2 ( медиана провед. к гипотенузе равна половине гипотенузы) , следовательно ΔAMC равнобедренный; ∠MCA = ∠MAC =20° .
∠MCH=∠MCA+∠MAC =20°+20°=40° (как внешний угол ΔAMC).
Из ΔCHM : ∠MCH =90° - ∠MHC=90° -40°=50° → В ;
СМ =AB/2 =(BC/sin∠MAC) /2 = 5/2sin20° → A ;
Из ΔBHC: CH =BC*sin∠B = 5sin70° → Г . [ ∠B=90° -∠A=90° -20°=70°