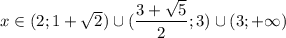ОДЗ логарифмов: x > 0, x ≠ 1, x > 2, x ≠ 3 ⇒ x > 2, x ≠ 3
Пусть . Тогда :
. Заметим, что t ≠ 0, так как это значение достигается только при x = 3 (x - 2 = x⁰ = 1 ⇔ x = 3). Но при x = 3 основание логарифма равно 1, что не удовлетворяет ОДЗ. Значит, домножим обе части дроби на t:
Решим методом интервалов:
+ - + +
----o----o----*---->
-1 -¹/₂ ¹/₂
Заметим, что по ОДЗ x > 2, то есть основание логарифма всегда больше 1. Значит, на ОДЗ неравенства равносильны:
Первое неравенство имеет решение (с учётом ОДЗ)
Второе неравенство раскладывается на множители:
Нули получившегося неравенства:
C учётом ОДЗ получаем, что в данном случае (левая граница меньше правой, так как √5 < 3).
Объединим промежутки. Сравним правую границу первого неравенства и левую границу второго. Сравним эти числа относительно 2,5:
задачи на вероятность можно решать по формулам и не понимать их а можно один раз понять и тогда формулы будут ненужны можете изучить мое решение и применить к нему формулы числовые ответы - правильные на 100%
первая деталь окажется бракованной в случае если первая деталь с первого автомата с вероятностью 0,8 она бракованная с вероятностью 0,01 или первая деталь с второго автомата с вероятностью 0,2 она бракованная с вероятностью 0,04 итого вероятность что первая взятая деталь бракованная 0,8*0,01+0,2*0,04 аналогично получаем вероятность что вторая взятая деталь бракованная 0,8*0,01+0,2*0,04 тогда вероятность что обе детали бракованные (0,8*0,01+0,2*0,04)*(0,8*0,01+0,2*0,04)= 0,000256 - ответ на первый вопрос теперь рассмотрим случай что бракованные детали изготовлены исключительно на первом автомате это значит что дважды с вероятностью 0,8 деталь была от первого автомата и каждый раз с вероятностью 0,01 попалась бракованная из всех деталей этого автомата вероятность такого события (0,8*0,01)*(0,8*0,01)= 0,000064 теперь посмотрим, каков вклад этой вероятности в вероятность что выбранные две детали оказались бракованными. (0,8*0,01)*(0,8*0,01) : (0,8*0,01+0,2*0,04)*(0,8*0,01+0,2*0,04) = 0,25 - искомый ответ 2 задания
произошло событие А вероятность которого оценивается как Р(А)=(0,8*0,01+0,2*0,04)*(0,8*0,01+0,2*0,04) вероятность того что это событие произошло именно по интересующему нас алгоритму Р(В)=(0,8*0,01)*(0,8*0,01) тогда условная вероятность (вероятность что произошло событие В при условии что состоялось событие А равна Р(В|А) =Р(В)/Р(А)=(0,8*0,01)*(0,8*0,01) : (0,8*0,01+0,2*0,04)*(0,8*0,01+0,2*0,04) = 0,25
задачи на вероятность можно решать по формулам и не понимать их а можно один раз понять и тогда формулы будут ненужны можете изучить мое решение и применить к нему формулы числовые ответы - правильные на 100%
первая деталь окажется бракованной в случае если первая деталь с первого автомата с вероятностью 0,8 она бракованная с вероятностью 0,01 или первая деталь с второго автомата с вероятностью 0,2 она бракованная с вероятностью 0,04 итого вероятность что первая взятая деталь бракованная 0,8*0,01+0,2*0,04 аналогично получаем вероятность что вторая взятая деталь бракованная 0,8*0,01+0,2*0,04 тогда вероятность что обе детали бракованные (0,8*0,01+0,2*0,04)*(0,8*0,01+0,2*0,04)= 0,000256 - ответ на первый вопрос теперь рассмотрим случай что бракованные детали изготовлены исключительно на первом автомате это значит что дважды с вероятностью 0,8 деталь была от первого автомата и каждый раз с вероятностью 0,01 попалась бракованная из всех деталей этого автомата вероятность такого события (0,8*0,01)*(0,8*0,01)= 0,000064 теперь посмотрим, каков вклад этой вероятности в вероятность что выбранные две детали оказались бракованными. (0,8*0,01)*(0,8*0,01) : (0,8*0,01+0,2*0,04)*(0,8*0,01+0,2*0,04) = 0,25 - искомый ответ 2 задания
произошло событие А вероятность которого оценивается как Р(А)=(0,8*0,01+0,2*0,04)*(0,8*0,01+0,2*0,04) вероятность того что это событие произошло именно по интересующему нас алгоритму Р(В)=(0,8*0,01)*(0,8*0,01) тогда условная вероятность (вероятность что произошло событие В при условии что состоялось событие А равна Р(В|А) =Р(В)/Р(А)=(0,8*0,01)*(0,8*0,01) : (0,8*0,01+0,2*0,04)*(0,8*0,01+0,2*0,04) = 0,25
Пошаговое объяснение:
ОДЗ логарифмов: x > 0, x ≠ 1, x > 2, x ≠ 3 ⇒ x > 2, x ≠ 3
Пусть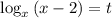 . Тогда
. Тогда 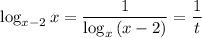 :
:
Решим методом интервалов:
+ - + +
----o----o----*---->
-1 -¹/₂ ¹/₂
Заметим, что по ОДЗ x > 2, то есть основание логарифма всегда больше 1. Значит, на ОДЗ неравенства равносильны:
Первое неравенство имеет решение (с учётом ОДЗ)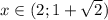
Второе неравенство раскладывается на множители:
Нули получившегося неравенства: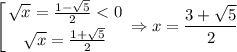
C учётом ОДЗ получаем, что в данном случае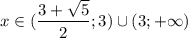 (левая граница меньше правой, так как √5 < 3).
(левая граница меньше правой, так как √5 < 3).
Объединим промежутки. Сравним правую границу первого неравенства и левую границу второго. Сравним эти числа относительно 2,5:
Тогда промежутки не пересекаются, итоговый ответ: