

f(x)' = ((x^3 – 4x)^4)’ = (x^3 – 4x)’ * ((x^3 – 4x)^4)’ = ((x^3)’ – (4x)’) * ((x^3 – 4x)^4)’ =
(3 * x^2 – 4) * 4 * (x^3 – 4x)^3 = 4 * (3x^2 – 4) * (x^3 – 4x)^3.
f(x)' = ((x + 1) / (x^2 + 1))’ = ((x + 1)’ * (x^2 + 1) - (x + 1) * (x^2 + 1)’) / (x^2 + 1)^2 = (((x)’ + (1)’) * (x^2 + 1) - (x + 1) * ((x^2)’ + (1)’)) / (x^2 + 1)^2 = ((1 + 0) * (x^2 + 1) - (x + 1) * (2x + 0)) / (x^2 + 1)^2 = (x^2 + 1 - 2x^2 - 2x) / (x^2 + 1)^2 = (-x^2 - 2x + 1) / (x^2 + 1)^2.
f(x)' = ((x^2) / (x^2 + 1))’ = ((x^2)’ * (x^2 + 1) - (x^2) * (x^2 + 1)’) / (x^2 + 1)^2 = ((x^2)’) * (x^2 + 1) - (x^2) * ((x^2)’ + (1)’)) / (x^2 + 1)^2 = (2x * (x^2 + 1) - (x^2) * (2x + 0)) / (x^2 + 1)^2 = (2x^3 + 2x - 2x^3) / (x^2 + 1)^2 = 2x / (x^2 + 1)^2.
f(x)' = ((x^3) / (x^2 + 5))’ = ((x^3)’ * (x^2 + 5) - (x^3) * (x^2 + 5)’) / (x^2 + 5)^2 = ((x^3)’) * (x^2 + 5) - (x^3) * ((x^2)’ + (5)’)) / (x^2 + 5)^2 = (3x^2 * (x^2 + 5) - (x^3) * (2x + 0)) / (x^2 + 5)^2 = (3x^4 + 15x^2 - 2x^4) / (x^2 + 5)^2 = (x^4 + 15x^2) / (x^2 + 5)^2.
Губки штангенциркуля плотно с небольшим усилием, без зазоров и перекосов прижимают к детали.
Определяя величину наружного диаметра цилиндра (вала, болта и т. д.), следят за тем, чтобы плоскость рамки была перпендикулярна его оси.
При измерении цилиндрических отверстий губки штангенциркуля располагают в диаметрально противоположных точках, которые можно найти, ориентируясь по максимальным показаниям шкалы. При этом плоскость рамки должна проходить через ось отверстия, т.е. не допускается измерение по хорде или под углом к оси.
Чтобы измерить глубину отверстия, штангу устанавливают у его края перпендикулярно поверхности детали. Линейку глубиномера выдвигают до упора в дно при подвижной рамки.
Полученный размер фиксируют стопорным винтом и определяют показания.
Пошаговое объяснение:
Задание3.
1) 3,5 км это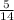
3,5 км : 5 · 14 = 9,8 км - длина всего участка.
ответ: 9,8 км
2) 5,6 км это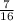
5,6 км : 7 · 16 = 12,8 км - длина всего участка.
ответ: 12,8 км
4) 13,5 км это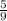
13,5 км : 5 · 9 = 12,8 км - длина всего участка.
ответ: 24,3 км