Question

мне. Мне нужно подробно! ​

Answer 1

324

Пошаговое объяснение:

Выберем некоторую точку функции y. Её координаты равны (x, 4x(6-x)²). Если спроецировать её на оси Ox, Oy, то мы попадём в другие вершины прямоугольника. То есть прямоугольник имеет стороны x, 4x(6-x)². Значит, площадь этого прямоугольника равна произведению сторон: S = 4x²(6-x)².

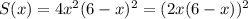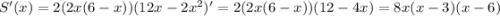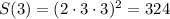Исследуем функцию площади прямоугольника $S(x)=4x^2(6-x)^2=(2x(6-x))^2$. Её производная $S'(x)=2(2x(6-x))(12x-2x^2)'=2(2x(6-x))(12-4x)=8x(x-3)(x-6)$. Точки экстремума — 0, 3, 6. В промежуток (0; 6) входит только точка 3. Если 0 < x < 3, S'(x) > 0, если 3 < x < 6, S'(x) < 0. Значит, x = 3 — точка максимума. Максимальная площадь прямоугольника равна $S(3)=(2\cdot 3\cdot 3)^2=324$.

Answer 2

Кому то может показаться, что излишне подробно, но это серьёзный пласт задач, хотел показать план работы