Заметим, что основание логарифма меньше единицы. Это означает, чтобы значение самого логарифма было больше ноля (как требуется в неравенстве), нужно, чтобы его подлогарифмическое выражение было тоже меньше единицы (и больше ноля, в силу области определения логарифмических выражений):
Все это можно довести до метода интервалов:
Первое неравенство можно решить так:
- - - + + +
____________________
Второе неравенство решается схожим образом:
- - - + + + - - -
___________________________ Или , или .
Как пересечение решений двух неравенств имеем решение .
Значит, наименьшее целое число, удовлетворяющее неравенству - это , что сходится с ответом.
Везде в решении: первое ведро объемом 13 л, второе - 9 л.
Наливаем 13-литровое ведро Выливаем 9 л во второе ведро, осталось 4 л Освобождаем второе ведро и переливаем в него 4 л (свободно 5 л) Наполняем первое ведро (13 л) и отливаем что можем во второе (5 л), осталось 8 л. Освобождаем второе ведро и переливаем в него 8 л (остался 1 л). Наливаем 13 л и отливаем 1 л во второе ведро - осталось 12 л. Освобождаем второе ведро. 12 л больше вместимости второго ведра. Поэтому отливаем 9 л, освобождаем второе ведро и сливаем в него оставшиеся 3 л. Свободно 6 л. Заполняем 13 л и отливаем 6 л во второе ведро. Осталось 7 л. Освобождаем ведро 9 л и сливаем туда 7 л из первого ведра. Наполняем 13 л, доливаем во второе 2 л, осталось 11 л. Освобождаем второе ведро. 11>9, поэтому выливаем 9 л с второго ведра. Осталось 2 л. Переливаем их во второе ведро. Набираем 13 л и отливаем 7 л во второе ведро. Осталось 6 л. --- Можно другим Набираем 9 л во второе ведро, переливаем все в первое, снова набираем второе и отливаем 4 л в первое: осталось 5 л во втором ведре. Освобождаем первое ведро, переливаем в него 5 л из второго, набираем второе. Переливаем 8 л в первое ведро, освобождаем его, оставшийся 1 л переливаем в первое ведро. Набираем 9 л, переливаем их в первое ведро (10 л стало), снова набираем 9 л и переливаем сколько можем (3 л.) Во втором ведре осталось 6 л.
Т. к. с уменьшением высоты ≈ 12 м давление увеличивается ≈ 1 мм. рт. ст., то давление у подножья горы высотой 1818 м., зная давление на вершине (570мм. рт. ст.), можно определить так:
1) 1818:12≈152 (мм. рт. ст.) - на столько увеличилось давление 2) 570+152=722 (мм. рт. ст.) - давление у подножья
Т. к. с уменьшением высоты ≈ 100 м. температура увеличивается ≈ 0,6°С, то температуру у подножья можно определить так:
1) 1818:100=18,18 2) 18,18×0,6≈11°С - увеличилась температура 3) -5+11=6°С - температура у подножья
Заметим, что основание логарифма меньше единицы. Это означает, чтобы значение самого логарифма было больше ноля (как требуется в неравенстве), нужно, чтобы его подлогарифмическое выражение было тоже меньше единицы (и больше ноля, в силу области определения логарифмических выражений):
меньше единицы. Это означает, чтобы значение самого логарифма было больше ноля (как требуется в неравенстве), нужно, чтобы его подлогарифмическое выражение было тоже меньше единицы (и больше ноля, в силу области определения логарифмических выражений):
Все это можно довести до метода интервалов:
Первое неравенство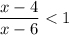 можно решить так:
можно решить так:
- - - + + +
__________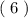 __________
__________ 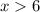
Второе неравенство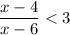 решается схожим образом:
решается схожим образом:
- - - + + + - - -
_________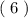 _________
_________ _________ Или
_________ Или 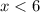 , или
, или 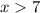 .
.
Как пересечение решений двух неравенств имеем решение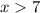 .
.
Значит, наименьшее целое число, удовлетворяющее неравенству - это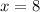 , что сходится с ответом.
, что сходится с ответом.
ответ: 8.