1) В треугольнике найти длину высоты АД , A(1;-14), B(3;-4), C (-6;8) .
Находим площадь треугольника ABC по формуле: S=(1/2)*|(Хв-Ха)*(Ус-Уа)-(Хс-Ха)*(Ув-Уа)| = 57 .
Находим длину стороны ВС, куда опущена высота АД.
BC (а)= √((Хc-Хв)²+(Ус-Ув)²) = 15
Тогда длина высоты равна
АД = 2S/ВС = 2*57/15 = 114/15 = 7,6 .
2) В треугольнике найти длину высоты АД , A(-11;10), B(-2;5), C (-10;-3).
Поступаем аналогично.
Площадь треугольника ABC
S=(1/2)*|(Хв-Ха)*(Ус-Уа)-(Хс-Ха)*(Ув-Уа)| = 56 .
BC (а)= √((Хc-Хв)²+(Ус-Ув)²) = √128 ≈ 11,31371.
Длина высоты равна:
АД = 2S/ВС = 2*56/√128 ≈ 9,8995.
1,5 км/ч - скорость течения реки.
Пошаговое объяснение:
Пусть скорость лодки равна x км/ч, а скорость течения - у км/ч
Составляем уравнение для случая, когда лодка плыла по течению реки:
(x + y) * 3 = 69
Составляем уравнение для случая, когда лодка плыла против течения реки:
(х - у) * 4 = 80
Решаем систему уравнения:
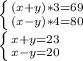
Выражаем из первого уравнения y и подставляем во второе уравнение:
y = 23 - x
--> x - (23 - x) = 20
Раскрываем скобки:
x - 23 + x = 20 --> 2x = 43 --> x=21,5 км/ч скорость лодки
Нам нужно найти скорость течения реки:
Подставляем х в любое из уравнений:
x + y = 23 --> 21,5 + y = 23 --> y = 23 - 21,5 = 1,5 км/ч - скорость течения реки.
ответ: 33 дерева растут в парке
решение
13+2=15 клёнов
15:3=5 елей
13+15+5=33 дерева