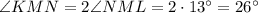Пошаговое объяснение:
Пусть x и y — сомножители числа 49, тогда xy = 49, и x = 49/y
Их сумма минимальна, т.е. минимально число z = x + y = 49/y + y.
Производная функции z' = -49/(y^2) + 1
Приравнивая её к нулю, находим её экстремумы
z' = -49/(y^2) + 1 = 0
z' = (y -7)(y + 7) / (y^2) = 0
y^2 = 49, y = 7 и y = -7
На числовой оси Oy производная z' больше нуля на интервале (-inf, -7) U (7, +inf)
На смежном интервале она меньше нуля, поэтому минимум её находится в точке y = 7.
На интервале положительных чисел (0, +inf) точка y = 7 представляет абсолютный минимум функции,
поэтому ответ x = 7, у = 7
1.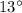
2.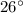
Пошаговое объяснение:
1.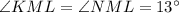
2.