1) и
✓
Наименьший общий знаменатель равен наименьшему общему кратному (НОК) знаменателей:
НОК(4; 6) = НОК(2·2; 2·3) = 2·2·3 = 12
✓
2) и
✓
НОК(4; 10) = НОК(2·2; 2·5) = 2·2·5 = 20
✓
3) и
НОК(6;8) = НОК(2·3;2·2·2) = 2·2·2·3 = 24
✓
4) и
✓
НОК(15;10) = НОК(3·5;2·5) = 2·3·5 = 30
-------------------------------------------------------------------
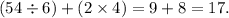
-------------------------------------------------------------------
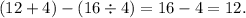
-------------------------------------------------------------------
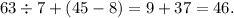
-------------------------------------------------------------------
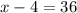
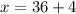
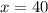
ответ : 40 .
-------------------------------------------------------------------

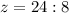
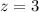
ответ : 3
-------------------------------------------------------------------
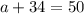
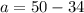
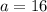
ответ : 16
-------------------------------------------------------------------
Решение 1
Преобразуем сумму в произведение по формуле
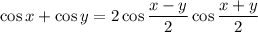
Попробуем получить что-нибудь похожее в правой части первого уравнения. Пригодятся формулы преобразования суммы косинусов в произведение и формула для косинуса двойного угла:
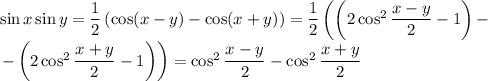
Таким образом, если обозначить косинус полусуммы за s, а косинус полуразности за a, получится система
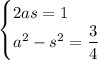
Из первого уравнения системы a = 1/(2s), подставляем во второе уравнение и после преобразований получаем биквадратное уравнение:
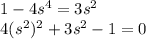
По теореме Виета угадываем, что 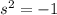 или
или 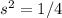 ; первый вариант не даёт вещественных решений, из второго следует
; первый вариант не даёт вещественных решений, из второго следует 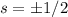 , тогда
, тогда  . Возвращаемся обратно к x и y:
. Возвращаемся обратно к x и y:
1) s = 1/2, a = 1:
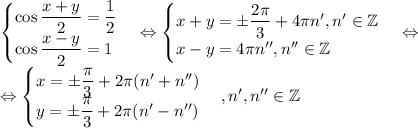
2) s = -1/2, a = -1:
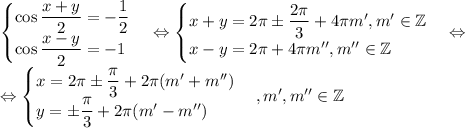
Можно переписать все полученные решения в виде
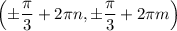 , где
, где 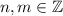 .
.
Решение 2
Возведём второе уравнение в квадрат, применим основное тригонометрическое тождество:
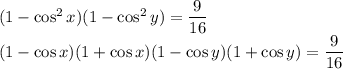
Из первого уравнения сумма косинусов 1, так что 1 - один косинус = другой косинус.
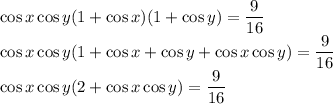
Получилось квадратное уравнение на cos x cos y, его корни -9/4 и 1/4. Произведение косинусов по модулю не больше 1, так что единственный вариант cos x cos y = 1/4. Совместно с cos x + cos y = 1 получаем, что соs x = cos y = 1/2, откуда 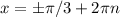 ,
, 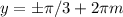 ,
, 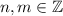 , знаки + и - выбираются независимо.
, знаки + и - выбираются независимо.
В этом решении был неравносильный переход при возведении в квадрат, могли появиться посторонние решения. Подставляя в исходную систему, получаем, что 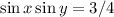 , только если в обоих значениях выбрать одинаковые знаки.
, только если в обоих значениях выбрать одинаковые знаки.
ответ
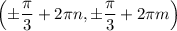 , где
, где 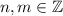
Пошаговое объяснение: