Объяснение:
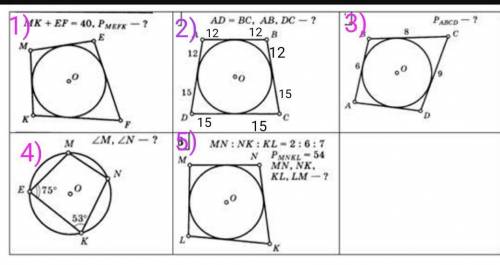
1)
В четырехугольник можно вписать окружность, если сумма противоположных сторон равна сумме двух других противоположных сторон.
МК+ЕF=ME+KF.
P=2(MK+EF)=2*40=80ед.
ответ: 80ед.
2)
АD=BC.
Две касательные проведенные из одной точки равны между собой.
АВ=2*12=24ед
DC=2*15=30ед.
ответ: АВ=24ед; DC=30ед.
3)
В четырехугольник можно вписать окружность, если сумма противоположных сторон равна сумме двух других противоположных сторон.
АВ+СD=BC+AD.
P=2(AB+CD)=2(6+9)=2*15=30ед.
ответ: 30ед.
4)
Четырехугольник можно вписать в окружность, если сумма противоположных углов равна 180°
<М+<К=180°. →
<К=180°-<К=180°-53°=127°
Аналогично для двух других углов
<Е+<N=180°
<N=180°-<E=180°-75°=105°
ответ: <К=127°; <N=105°
5)
В четырехугольник можно вписать окружность если сумма противоположных сторон равна сумме двух других противоположных сторон
MN+KL=P/2
Пусть MN=2x; KL=7x.
Уравнение
2х+7х=54/2
9х=27
х=3
МN=2x=2*3=6ед.
KL=7x=7*3=21ед.
NK=6x=6*3=18ед.
LM=(MN+KL-NK)=6+21-18=9ед.
ответ: MN=6ед; KL=21ед; NK=18ед; LM=9ед.
а где продолжение условия? основанием пирамиды dabc является правильный треугольник abc сторона которого = ребро da перпендикулярно к плоскости авс , а плоскость dbc составляет с плоскостью авс угол 30*. найдите площадь боковой поверхности пирамиды. условие такое? если такое, то вот решение : s(бок) = 2s(адс) + s(всд) угол дка = 30, тогда ад = ак* tg30 = (av3/2)*v3/3 =a/2 тогда s(асд) = 1/2*а*а/2 = а^2 / 4 дк = а, тогда s(всд) = 1/2*а*а = а^2 / 2 s(бок) = 2*(а^2 / 4) * (а^2 / 2) = а^2