Это парабола, ветви направлены вверх и она всегда положительна на всей оси Ох, только в точке k=1 принимает значения 0, значит k принимает все значения, кроме 1
аналогично для второго уравнения, тот же дискриминант и >0
Поскольку весы именно чашечные, то задача нахождения фальшивой монеты из N сводится к бинарному поиску - мы каждый раз делим исходную кучку пополам (или на три части, если пополам не делится), определяем ту, которая легче, затем поступаем с ней аналогично. И т.д. пока сравнение не сведется к 2-м монетам - более легкая из них и есть искомая. При этом для N монет нам понадобится log2(N) взвешиваний. Если N не степень двойки, то округление идет до ближайшей СЛЕДУЮЩЕЙ. Т.о. в нашем примере log2(N) = 4. Откуда N = 2^4 = 16. 16 монет.
Купили одинаковое количество книг по цене 76 рублей и по цене 49 рублей. За все книги по цене 76 рублей заплатили 684 рубля. рублей купили? Какова общая стоимость всей покупки? Решение: 1) 684 : 76 = 9(книг) купили по цене 76 рублей, значит столько же купили книг по цене 49 рублей. 2) 49 * 9 = 441 (рубль) заплатили за 9 книг по цене 49 рублей 3) 684 + 441 =1125 (рублей) заплатили всего ответ; 1125 рублей - общая стоимость покупки. Таблица будет выглядеть так: цена кол-во стоимость 76руб 9 684руб } 1125 руб.- общая стоимость 49руб 9 441руб
k∈(-∞;1)∪(1;+∞)
Пошаговое объяснение:
Раскрываем модуль по определению:
Уравнение имеет 2 решения, если дискриминант >0
D=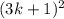 -4(2k²+2k)>0
-4(2k²+2k)>0
9k²+6k+1-8k²-8k>0
k²-2k+1>0
(k-1)²>0
Это парабола, ветви направлены вверх и она всегда положительна на всей оси Ох, только в точке k=1 принимает значения 0, значит k принимает все значения, кроме 1
аналогично для второго уравнения, тот же дискриминант и >0
ответ: k∈(-∞;1)∪(1;+∞)