
Объяснение:
№1 фото
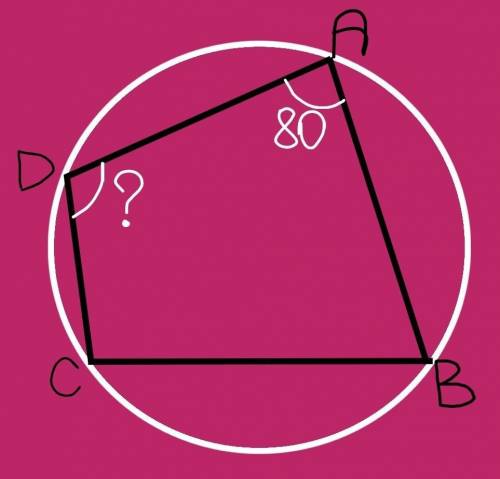
Условие некорректно! Скорее всего надо было найти угол С.
Около четырехугольника можно описать окружность, если сумма его противоположных углов равна 180°.
Углу А противоположен угол С, тогда угол С=180°–угол А=180°–80°=100°.
ответ: б) 100°
Найти угол D, незная угол В или не имея других данных, невозможно.
№2
Около четырехугольника можно описать окружность, если сумма его противоположных углов равна 180°.
Тогда угол CDA=180°–угол АВС=180°–110°=70°.
Сумма углов в любом треугольнике равна 180°.
Следовательно угол ACD=180°–угол CAD–угол CDA=180°–50°–70°=60°
ответ: в) 60°
№3
В четырехугольник можно вписать окружность, если суммы его противоположных сторон равны.
Тоесть ВС+AD=AB+CD
Пусть АВ=4n, тогда CD=3n.
Подставим значения в уравнение:
13+22=4n+3n
35=7n
n=5
Тогда CD=3*5=15 см
ответ: а) 15 см.
36:3=12.
Опустим высоту в треугольнике до пересечения с окружностью. Соединим полученную точку с одной из оставших вершин заданного треугольника. Получим прямоугольный треугольник, гипотенуза которого является диаметром окружности. Угол между высотой треугольника и его стороной равен 30°. Высота в правильном треугольнике является и биссектрисой и медианой. 60°:2=30°.
Вычислим диаметр окружности:
d=12:cos30°=12:(√3/2)=24/√3=24·√3/√3·√3=24√3/3=8√3.
Диагональю квадрата является диаметр окружности. Обозачим сторону квадрата через а.
По теореме Пифагора: a²+a²=d², 2a²=(8√3)².
2a²=64·3,
a²=32·3=16·2·3,
a=√16·6=4√6.
a=4√6.