Question

сторона, перпендикулярная диагональной стороне равносторонней трапеции b, образует угол α с большим основанием. найти поверхность тела, образованную вращением вокруг большого основания трапеции​

Answer 1

ответ: $S=4\pi b^2*tg(a)*cos^2(\frac{a}{2})*(2cos(a)+1)$

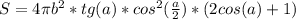
Пошаговое объяснение:

Опускаем высоты BL и СR, тогда:

$AL=RD=bcos(a)\\AD=\frac{b}{cos(a)}\\BC= LR = AD-2AL = \frac{b}{cos(a)} -2bcos(a) = b(\frac{1}{cos(a)} -2cos(a))=\\=b\frac{1-2cos^2(a)}{cos(a)}$

При вращении данной трапеции вокруг большего основания получаем два конуса с образующими равными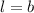 $l=b$ основанием c радиусом 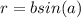$r=bsin(a)$, а также цилиндром с тем же самым радиусом основания и высотой $h=BC=b\frac{1-2cos^2(a)}{cos(a)}$ .

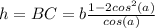Площадь боковой поверхности конуса: $S_{1} =\pi rl$

Площадь боковой поверхности цилиндра: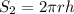 $S_{2} =2\pi rh$

Тогда площадь боковой поверхности всей фигуры:

$S=\pi r (2l +2h)=2\pi bsin(a)(b+b\frac{1-2cos^2(a)}{cos(a)}) = 2\pi b^2\frac{(sin(a))(cos(a)+1-2cos^2(a))}{cos(a)} =\\=2\pi b^2\frac{sin(a)(1-cos(a))(2cos(a)+1)}{cos(a)} =4\pi b^2*tg(a)*cos^2(\frac{a}{2})*(2cos(a)+1)$