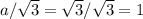

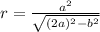
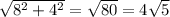

Один из вариантов решения задачи:
16 снежинок , нужно разложить на 4 стены: например так: 5-2-3-6; или так: 7-6-1-2, при таком "раскладе" сумма колич. снежинок на противоположных сторонах равна восьми. Колличество вариантов можно посчитать, разложив число 8 на всевозможные слагаемые, т.е.: 1+7(каждое из этих слагаемых и является колличеством снежинок на каждой из противоположных стен); 2+6; 3+5. Из этого следует, что возможно,например, 3 варианта выполнения этого задания. (3-1-5-7); (5-2-3-6); (7-6-1-2).
PS: но может и больше.
_5_
6 I___I 2
3
ответ:(kx)'=k
(\ln x)'= \frac{1}{x}
y=10x-10\ln(x+7)+5 y'=10- \frac{10}{x+7} y'=0 10- {10}{x+7} =0 1-1}{x+7} =0 \\ {1}{x+7} =1 x+7=1 x_{min}=-6
Если интересует сам минимум, то:
y_{min}=y(x_{min})=10\cdot(-6)-10\ln(-6+7)+5=-60+5=-55
ответ: точка минимума х=-6
Пошаговое объяснение: