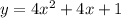
1)
ОДЗ : x ∈ R
2)
Область значений : y ≥ 0
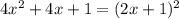
Квадратный трехчлен имеет один корень и ветви параболы смотрят вверх, значит y ≥ ордината вершины => y ≥ 0
3)
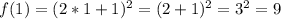
4)
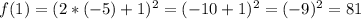
5)
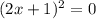
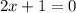
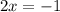

Нули : x = -0.5
6)
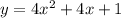
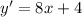
Отрезок возрастания (y' ≥ 0) :
8x + 4 ≥ 0
8x ≥ -4
x ≥ -0.5
Отрезок спадания (y'≤ 0) :
8x + 4 ≤ 0
8x ≤ -4
x ≤ -0.5
Когда Даша не решает 3- задачу, но решает она получает +
очевидно, что если Д решила столько же пятибалльных задач, сколько и М, то набрать двумя дополнительными задачами только ей не удастся, так как решение задач в даст +8, а если она не решила трехбалльную, а вместо нее решила четырех то тогда она получит еще плюс +1 итого +9 и разрыв будет только увеличиваться. Еще хуже будет если она решит дополнительную пятибалльную, тогда у нее уже будет перебор на след задаче.
Значит Д решила меньше 4 пятибалльных задач.
предположим, что Д решила 0 пятибалльных задач
значит Д теряет которые, она может восполнить решив 5*четырехбалльных задач
теперь ей нужно набрать 1 задачей
займем задачу у трехбалльных,
Д решила 9 трехбалльных, но еще 2 четырехбалльных, то есть наберёт 4-3+4=5 очков.
то есть значит Д решила 0 пятибалльных, на 7 больше четырех , и не решила одну трехбалльную
Возможно так как трехбалльных задач всего 10, то и остальных тоже по 10, так что этот вариант не подойдет, так как получается что всего 4+7=11 четырехбалльных задач...
тогда Даша решила 1 пятибалльную задачу
недобрала - на них, но решила 5 четырехбалльных, то есть набрала -15+20=+ (итого 9+ четырехбалльных задач)
Этот вариант подходит, 10 трехбалльных 1 пятибалльная и 5+4 четырехбалльных
если Даша решила 2 пятибалльные задачи
то - решает 4 четырехбалльных и получает -10+16=+6
что уже перебор.
значит 3 пятибалльных тоже не подойдет.
ответ 1 задачу.
Если я верно понимаю, что интервал (100; 20000) включает в себя все числа между 100 и 20000, но исключая концы, то:
ответ: 19891.
(НОК(a, b) = [a, b] (в моём случае - [a; b]))
Пусть в требуемом виде нужно представить число i = 2^t * (2p + 1):
а) p > 0. Тогда возьмём следующие числа: k = p * 2^t; n = m = 2^t.
[p * 2^t ; 2^t] + [p * 2^t ; 2^t] + [2^t ; 2^t] = p * 2^t + p * 2^t + 2^t = 2^t * (2p + 1)
Значит, при p > 0 представление существует.
б) p = 0. Докажем, что в таком случае решения не существует. Пусть k = 2^a * k' ; m = 2^b * m' ; n = 2^c * n'. Тогда k', m', n' не могут иметь общих множителей (иначе бы этот множитель присутствовал во всех трёх слагаемых, но отсутствовал бы в правой части (этот множитель - не 2, так как иначе увеличим показатели степеней)). Пусть a ≥ b ≥ c (иначе переобозначим), тогда:
[2^a * k' ; 2^b * m'] + [2^b * m' ; 2^c * n'] + [2^c * n'; 2^a * k'] = 2^t
2^a * k' * m' + 2^a * n' * k' + 2^b * m' * n' = 2^t
2^b * (2^(a-b) * k' * m' + 2^(a-b) * k' * n' + m' * n') = 2^t
2^(a-b) * k' * m' + 2^(a-b) * k' * n' + m' * n' = 2^(t - b)
Далее возможны две ситуации:
1) a = b, тогда слева три нечётных числа, а справа либо чётное число, либо 1.
2) a > b, тогда слева два чётных числа и одно нечётное, а справа либо чётное число, либо 1.
Значит, при p = 0 решений нет.
Осталось заметить, что в промежутке от 100 до 20000 всего 8 степеней двойки.
...............................