
12 см²
Пошаговое объяснение:
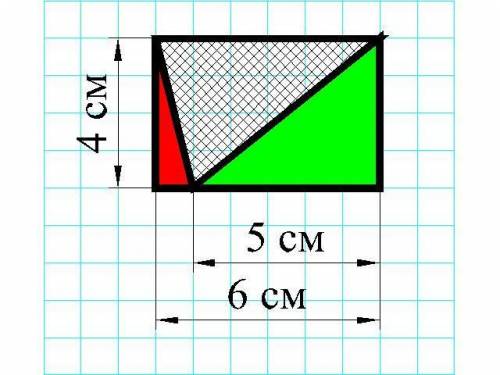
Найдем площадь прямоугольника со сторонами 6 см и 4 см
S прямоугольника = 6*4 = 24 (см²)
Найдем площадь красного прямоугольного треугольника (см. первую картинку) с катетами 4 см и 1 см
S кр.тр. = 4*1:2 = 2 (см²)
Найдем площадь зеленого прямоугольного треугольника с катетами 4 см и 5 см
S зел.тр. = 4*5:2 = 10 (см²)
Найдем площадь данной фигуры:
S фигуры = S прямоугольника - S кр.тр. - S зел.тр. = 24 - 2 - 10 = 12 (см²)
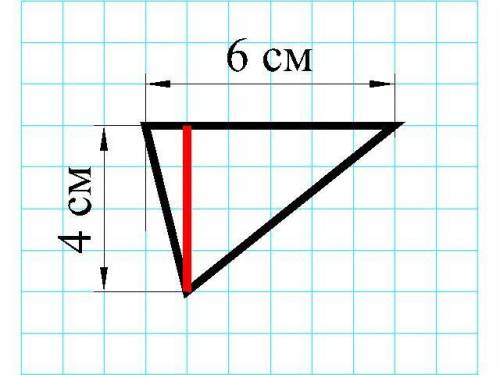
ИЛИ (не знаю, в каком Вы классе, более взрослый вариант):
Рассмотрим данный треугольник (вторая картинка):
Один катет = 6 см, а перпендикуляр (красная линия) = 4 см
S фигуры = 6*4:2 =12 (см²)
ответ: -2/3.
Пошаговое объяснение:
Положим x-π/3=t, тогда x=t+π/3 и при x⇒π/3 t⇒0. Тогда данный предел можно записать в виде lim [√3-sin(t)-√3*cos(t)]/sin(3*t/2), где t⇒0. Но так как √3-√3*cos(t)=√3*[1-cos(t)]=2*√3*sin²(t/2), то этот предел можно записать в виде lim[-sin(t)+2*√3*sin²(t/2)]/sin(3*t/2), где t⇒0. Но при t⇒0 бесконечно малые величины sin(t), sin²(t/2) и sin(3*t/2) можно заменить эквивалентными бесконечно малыми t, (t/2)²=t²/4 и 3*t/2 соответственно, так что данный предел примет вид 2/3*lim [-t+√3*t²/2]/t=2/3*lim(-t/t)+1/√3*lim(t²/t)=-2/3+1/√3*lim(t), где t⇒0. Отсюда искомый предел равен -2/3.
Проведём проверку по правилу Лопиталя: [2*sin(x)-√3]'=2*cos(x), а [cos(3*x/2)]'=-3/2*sin(3*x/2). При x⇒π/3 первое выражение стремится к 1, а второе - к -3/2. Поэтому их отношение стремится к 1/(-3/2)=-2/3, что совпадает с полученным ответом.
1) (√a - 5)(√a+5) = (√a)²-5² = a-25
Подставляем значение:
25,2-25 = 0,2
2) 16ab+2*(-a+4b) = 16ab+2*((-a)²+2*(-a)*(4b)+(4b)²) = 16ab+2*(a²-8ab+16b²) = 16ab+2a²-16ab+32b² = 2a²+32b² = 2*(a²+16b²)
Подставляем значения:
2*((√3)²+16*(√5)²) = 2*(3+80)=166
3)
Подставляем значения:
4)
Подставляем значения:
5)
Подставляем значения:
1,8 : 0,9 = 2
6)
Подставляем значения:
-2,3-4 = -6,3