Условие задачи не совсем корректно. Должен быть дан и рисунок.
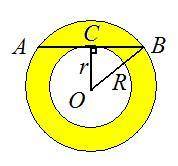
Условие. Дано кольцо (см. рис.). Хорда АВ касается меньшей окружности и равна 8 см. Найдите площадь кольца.
Решение. Пусть О - центр данных окружностей.
Опустим из точки О перпендикуляр к АВ в точку касания С.
В ΔВОС катет ОС = r (r - радиус меньшей окружности), а гипотенуза ОВ = R (R - радиус большей окружности).
По теореме Пифагора СВ² = ОВ² - ОС² = R² - r².
С другой стороны, СВ = 1/2 · АВ = 1/2 · 8 = 4 (см), т.к. ΔАОВ - равнобедренный (ОА = ОВ = R) и ОС является не только высотой, но и медианой.
Значит, R² - r² = 4² = 16 (см²).
Площадь кольца равна: S = πR² - πr² = π(R² - r²) = π · 16 = 16π (см²).
ответ: 16π см².
См. рис. в прикрепленном файле
50*25+ 2(25*30+50*30)= 1250+ 2(750+1500)=1250+2*2250=5750
Решение по действиям:
1)50*25=1250 (см кв) - площадь основания
2)2(50+25)=150 (см кв) - периметр основания
3)150*30=4500 (см кв) - произведение периметра основания и высоты, т.е. площадь боковой поверхности
4)1250+4500=5750 (см кв) - площадь поверхности стекла
5750см кв=57,5 дм кв
Ещё один
1)Находим полную поверхность параллелипипеда
2)Вычитаем из неё поверхность основания