Дұрыс емес❌ооогг
Пошаговое объяснение:
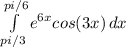
здесь получится рекурсивный интеграл. поэтому сначала решаем неопределенный интеграл
схема такая: два раза будем интегрировать по частям
формула интегрирования по частям
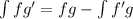
итак, первый раз
f = cos(3x) ⇒ f' = -3sin(3x)
g'= e⁶ˣ ⇒ g = (e⁶ˣ )/6
тогда
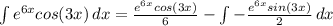
теперь второй раз интегрируем получившийся справа интеграл
f = -3sin(3x) ⇒ f' = -9cos(3x)
g' = (e⁶ˣ )/6 ⇒ g = (e⁶ˣ )/36
тогда
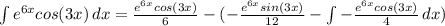
или
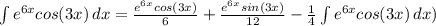
вот, мы видим, что исходный интеграл повторился. теперь у нас вроде как уравнение относительно этого интеграла. решим его и получим
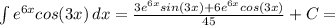
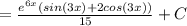
теперь осталось только подставить пределы интегрирования
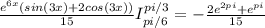
всё. это ответ
1)х:2=2:5
5х=2×2
5х=4
х=4:5
х=0.8
2)х:18=7:9
9х=18×7
9х=126
х=126:9
х=14
3)х:18=2:3
3х=18×2
3х=36
х=36:3
х=12
4)6:х=3:7
3х=6×7
3х=42
х=42:3
х=14
5)5:9=15:х
5х=15×9
5х=135
х=135:5
х=27
6) 12:7=60:х
12х=7×60
12х=420
х=420:12
х=35