Чтобы из числа можно было сделать все шесть различных двухзначных чисел, необходимо, чтобы исходное число было трехзначным и все цифры в нем были разные, представим это число в виде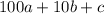 
.
А сумма всех шести различных двухзначных чисел будет такая:
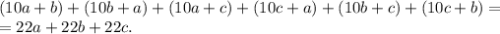
При этом (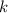
натуральное):
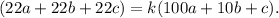
Представим теперь, что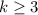 
, то есть:
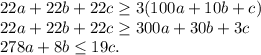
Но это противоречие, так как правая часть по-любому больше левой, а здесь она меньше. Поэтому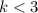 
.
Итак, нужно рассмотреть два случая:
1). 
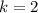. Тогда:
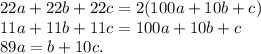
Нетрудно понять, что в натуральных однозначных числах здесь всего одно решение: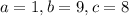 
.
А нужное число - это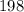 
.
2). Случай посложнее: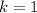 
.
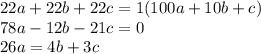
Если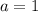 
уравнение принимает вид 
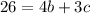, и, тогда в вышеуказанных условиях у него такое одно решение: 
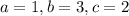. Число - 
.
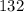Ну а теперь пусть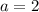 
и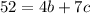 
. Здесь методом подбора: 
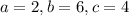. А число - 
.
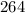И последний случай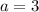 
, то есть 
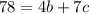, где, подбором, 
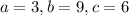. Число 
.
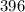Делаем вывод, что Вася богатый и у него в доме четыре (по крайней мере!) квартиры.
Парабола y=x² проходит выше прямой y=2x-3.
Вычтем первого уравнения второе и получим функцию зависимости расстояния по оси у между заданными линиями:
f(x) = x²-2x+3.
Найдём производную этой функции для определения экстремума.
f'(x) = 2x-2.
Приравняем нулю:
2х - 2 = 0.
х = 2/1 = 1.
Найдём знаки производной f'(x) = 2x-2.
Где производная положительна - функция возрастает, где отрицательна - там убывает.
Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точка минимума.
х = 0 1 2
y' = -2 0 2.
Поэтому в точке х=1 имеем минимум функции.
Если по оси у расстояние между линиями минимально, то оно и по оси х будет тоже минимальным.
Находим вертикальное расстояние по разности ординат:
параболы у1 = 1² = 1,
прямой у2 = 2*1-3 = -1.
Δу = 1-(-1) = 2.
Расстояние d по перпендикуляру к прямой равно:
d = Δy*cos α.
Тангенс угла наклона прямой к оси Ох равен 2 (по уравнению у = кх + в, где к это тангенс угла).
cos α = 1/√(1+tg²α) = 1/√(1+4) = 1/√5 = √5/5.
Отсюда получаем ответ:
d = 2*(√5/5) = 2√5/5 ≈ 0,894427.
Аналогичный ответ можно получить, если точку минимального расстояния от параболы до прямой найти с касательной, угловой коэффициент (и значение производной) которой равен 2 (как у заданной прямой).
Получаем 2х = 2, х = 1. Это точка с минимальным расстоянием до прямой 2х - 3.
Далее через точку х = 1 проводим нормаль к прямой и ищем точку пересечения. По разности координат находим длину перпендикуляра - то есть наименьшего расстояния.
Пошаговое объяснение:
Окружность - кривая замкнутая линия, все точки которой одинаково удалены от одной точки, называемой центром