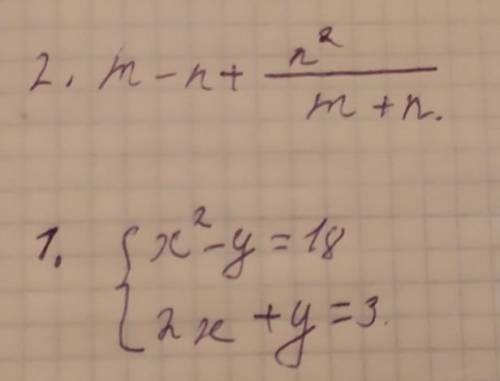
Пошаговое объяснение:
Чтобы записать смешанную периодическую дробь в виде обыкновенной, надо из числа, стоящего до второго периода вычесть число, стоящее до первого периода, результат записать в числителе; в знаменатель записать число, содержащее столько девяток, сколько цифр в периоде, и столько нулей в конце, сколько цифр между запятой и периодом.
1) 0,9(4)= (94-9)/90=85/90=17/18
2) 1,23(12)= 1 (2312-23)/9900=1 2289/9900=1 763/3300
3) 4, 01(11)= 4( 111-1)/9900= 4 110/9900= 4 11/990= 4 1/90
4) 14,14(303)=14 (14303-14))99900=14 14289/99900=14 4763/33300
Пошаговое объяснение:
1) Перенесите запятую так,чтобы каждое из данных чисел содержало 5 целых:500,1;0,56;56,7;0,0592;53. -Во сколько раз изменилось данное число?
500,1⇒5,001
500,1 : 5,001= 100
число уменьшилось в 100 раз
0,56 ⇒5,6
5,6 : 0,56= 10
число увеличилось в 10 раз
56,7 ⇒5,67
56,7 : 5,67=10
число уменьшилось в 10 раз
0,0592⇒5,92
5,92 : 0,0592= 100
число увеличилось в 100 раз
53⇒5,3
53: 5,3=10
число уменьшилось в 10 раз
2) Представьте в виде десятичной дроби:
1) 3/10= 3:10=0,3
2) 7 15/1000= 7 + ( 15 : 1000)= 7+0,015=7,015
3) 1, 7 = 1 7/10
10 ,007 = 10 7/1000
4) 34 : 100=0,34
0,012 *10= 0,12
В решении.
Пошаговое объяснение:
1)Упростить:
m-n+n²/(m+n)=
Общий знаменатель (m+n):
=[(m+n)*m-(m+n)*n+n²]/(m+n)=
=(m²+mn-mn-n²+n²)/(m+n)=
=m²/(m+n).
2)Решить систему уравнений:
х²-у=18
2х+у=3
Выразить у через х во втором уравнении, подставить выражение в первое уравнение и вычислить х:
у=3-2х
х²-(3-2х)=18
х²-3+2х=18
х²+2х-21=18, квадратное уравнение, ищем корни:
D=b²-4ac =4+84=88 √D= √4*22=2√22;
х₁=(-b-√D)/2a
х₁=(-2-2√22)/2
х₁= -1-√22;
х₂=(-b+√D)/2a
х₂=(-2+2√22)/2
х₂= -1+√22.
у=3-2х
у₁=3-2х₁
у₁=3-2(-1-√22)
у₁=3+2+2√22
у₁=5+2√22;
у₂=3-2х₂
у₂=3-2(-1+√22)
у₂=3+2-2√22
у₂=5-2√22.
Решение системы уравнений (-1-√22; 5+2√22); (-1+√22; 5-2√22).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.