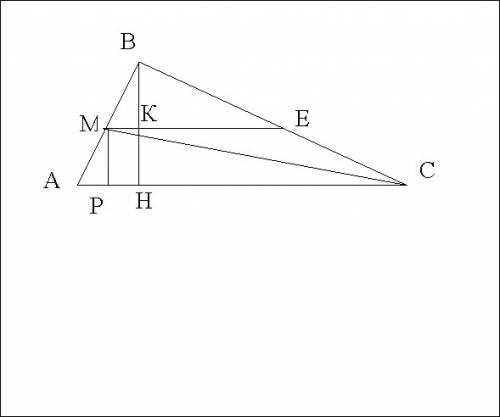
Дано
Δ АВС
ВН ┴АС
ВН=10 см
АН=4 см
НС = 10 см
АМ = МВ
Найти СМ
Решение
1) Проведём МР║ВН.
Для Δ АВН - это средняя линия, т.к. проходит через середины сторон АВ и АН.
Значит, МР = ВН/2 =10/2=5см.
2) Проведём МЕ║АС.
Для Δ АВН отрезок МК - это средняя линия, т.к. проходит через середины сторон АВ и ВС.
Значит, МК = АН/2 =4/2=2см.
В прямоугольнике МРНК противоположные стороны равны, т.е.
МК = РН = 2 см.
Отрезок РС = РН + НС = 2см + 10 см = 12 см
3) Из прямоугольного Δ МРС по теореме Пифагора найдём гипотенузу МС.
МС² = МР² +РС²
МС² = 5² + 12²2 = 25 + 144 = 169
МC= √169 =13 см
ответ: МС =13 см
1 дециметр-0,1 м
Увеличим диаметр каждой из окружностей на 2 дециметра (0,2 м)
0,4 м - одна окружность
0,5 м - вторая окружность
6 м (60 дециметров) разделим на диаметр каждой окружности и получим число оборотов каждого цилиндра, которое им понадобится для прохождения всего пути.
1) 6:0,4=15 оборотов
2) 6:0,5=12 оборотов
ответ: число оборотов первого цилиндра на 3 больше второго.