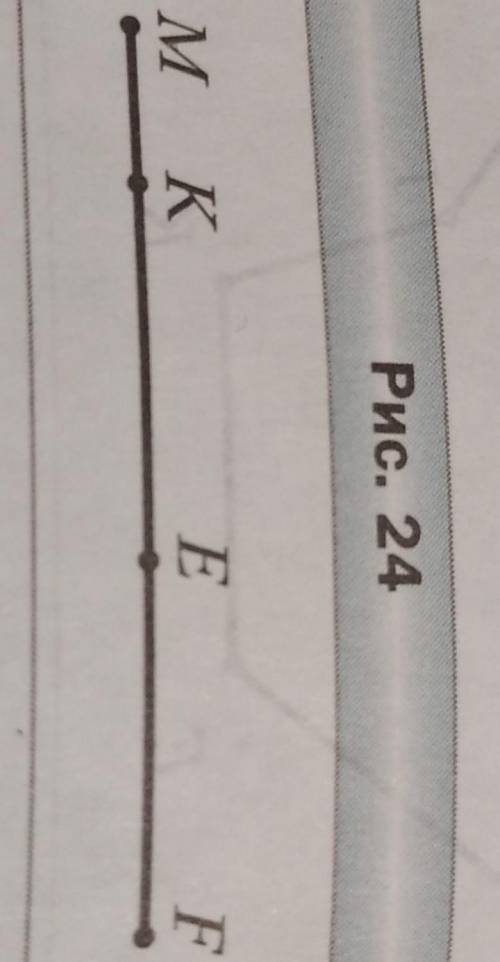
№ 1.
Пусть х дм - одна сторона треугольника, тогда 3х дм - другая сторона, (х + 23) дм - третья сторона. Периметр треугольника равен 108 дм. Уравнение:
х + 3х + х + 23 = 108
5х = 108 - 23
5х = 85
х = 85 : 5
х = 17 (дм) - одна сторона
3х = 3 · 17 = 51 (дм) - другая сторона
х + 23 = 17 + 23 = 40 (дм) - третья сторона
Вiдповiдь: 17 дм, 51 дм i 40 дм.
№ 2.
Пусть а = х см - длина, тогда b = (х - 3,8) см - ширина. Периметр прямоугольника равен 12,4 см. Уравнение:
(х + х - 3,8) · 2 = 12,4
2х - 3,8 = 12,4 : 2
2х - 3,8 = 6,2
2х = 6,2 + 3,8
2х = 10
х = 10 : 2
х = 5 (см) - длина а
5 - 3,8 = 1,2 (см) - ширина b
S = a · b = 5 · 1,2 = 6 см² - площадь прямоугольника
Вiдповiдь: 6 см².
507. Дано: ΔABC, CH і AT — висоти, AB = 8 см, ВС = 6 см, СН = 3 см. Знайти АТ.
Площа трикутника рівна половині добутку сторони на висоту, проведену на цю сторону.
Знайдемо площу трикутника ΔABC:
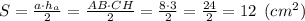
Виразимо іншу висоту через цю ж формулу:
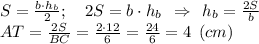
Відповідь: АТ = 4 см.
508. Дано: ΔEFS — рівнобедрений, EF — основа, EF = 40 см, SF = 29 см. Знайти S(EFS).
SF = SE = 29 см, так як ΔEFS — рівнобедрений.
Проведемо висоту SH до основи тр-ка. Висота у рівнобедреному тр-ку є медіаною, тому EH = FH = 40/2 = 20 см.
Знайдемо катет SH з ΔESH (∠EHS = 90°) за т. Піфагора:
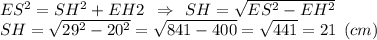
Підставимо значення у формулу площі трикутрина:
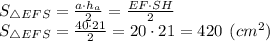
Відповідь: Площа ΔEFS рівна 420 см².

MF=43 см
ME=26см
KE=18см
MK-?
EF-?
Решение
MF-ME
43-26=17см-EF
ME-KE
26-18=8см-MK
EF+MK+KE
17+8+18=43см
ответ:МК-8 см,ЕF-17см