Пошаговое объяснение:
Решение прикреплено

ответ: 14 детей.
Пошаговое объяснение:
Число детей , у кого на ногах поровну носков, в 4 раза меньше, чем тех, у кого не поровну, значит : было 1/5 детей, у кого на ногах поровну носков и 4/5 детей, у кого не поровну. Когда каждый ребенок снял носок с одной ноги и надел на другую, то детей, у кого носков поровну стало в 2 раза меньше, чем тех, у кого не поровну, значит: стало 1/3 детей, у кого на ногах поровну носков и 2/3 детей, у кого не поровну.
Найдем НОК знаменателей:
НОК(3;5)=15 ; Т.к всего детей меньше 35, и вычисления должны быть в натуральных числах , то наибольшее число детей будет:
15*2=30 (детей) это наибольшее количество детей, которые пошли на прогулку.
30*(1/5)=6 (детей) у кого на ногах было вначале носков поровну. (После переодевания количество носков стало отличаться на 2.)
30*(1/3)=10 (детей) у кого на ногах стало после переодевания носков поровну. (В начале количество носков отличалось на 2.)
30-(6+10)=14 (детей) это наибольшее количество детей в начале прогулки, число носков на ногах которых могло отличаться на 1.
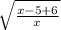 ?
?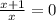

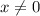
Т.к по данным нам известно что: А(5), В(2), С(4), D(8) то ресуем координатный луч и ставим буквы.