Формулы приведения работают так: надо определить, какой будет знак (если угол a в первой четверти), поставить его, а потом поменять название на кофункцию, если прибавляется или вычитается нечетное число π/2 (или 90°), и оставить название, если целое число π (180°).
1) Если повернуть угол α на π/2, получится угол II четверти, в ней синус положителен. Прибавляли π/2, sin меняем на cos.
sin(π/2 + α) = cos α
2) Прибавление 2π — поворот на полный круг, получаем угол -α из IV четверти. в ней косинус положителен. Поворот на целое число π, не меняем название функции.
cos(π - α) = cos α
3) угол из IV четверти, ctg < 0, название не меняется
ctg(360° - α) = -ctg α
4) III четверть, cos < 0, название меняется
cos(3π/2 + α) = -sin α
5) Прибавлние полного оборота ничего не меняет.
sin(2π + α) = sin α
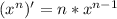 несколько раз.
несколько раз.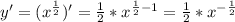
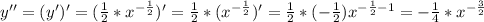
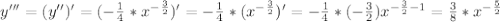
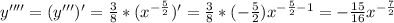
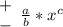
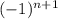
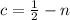
3) Ни одна высота этого треугольника не имеет целочисленной длины.
Пошаговое объяснение:
Сам только что решил и перепроверил.