3,72х + 0,13х = 6,16
3,85х = 6,16
х = 6,16 : 3,85
х = 1,6
проверка:
3,72 * 1,6 + 0,13 * 1,6 = 5,952 + 0,208 = 6,16; 6,16 = 6,16 - верно
4,7х - 1,2х + 3,7 = 8,6
3,5х + 3,7 = 8,6
3,5х = 8,6 - 3,7
3,5х = 4,9
х = 4,9 : 3,5
х = 1,4
проверка: 4,7 * 1,4 - 1,2 * 1,4 + 3,7 = 6,58 - 1,68 + 3,7 = 4,9 + 3,7 = 8,6
8,6 = 8,6 - верно
4,5 * ( х - 2,9 ) = 1,35 ( обе части разделим на 4,5)
х - 2,9 = 0,3
х = 0,3 + 2,9
х = 3,2
проверка: 4,5 * ( 3,2 - 2,9 ) = 4,5 * 0,3 = 1,35; 1,35 = 1,35 - верно
( 2х - 7 ) : 0,02 = 100
2х - 7 = 100 * 0,02
2х - 7 = 2
2х = 2+7
2х = 9
х = 9 : 2
х = 4,5
проверка: ( 2 * 4,5 - 7 ) : 0,02 = ( 9 - 7 ) : 0,02 = 2 : 0,02 = 100
100 = 100 - верно
1)
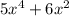
2)
функция - не монотонная
экстремумы: (-6; 540), (8; -832)
3)
минимум f(4)= -1
максимум f(2)=3
Пошаговое объяснение:
1)
просто диференцируем по частям
2)
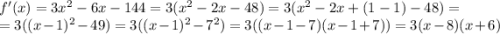
это производная исходной функции
как бы тут уже видно, что производная:
квадратичная парабола,
роги вверх,
знак меняет (а это значит, что исходная функция - не монотонная) в точках: x1 = -6; x2 = 8. это и будут точки экстремумов
минимум и максимум производной нас не интересуют
Решаем уравнение
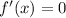
3(x-8)(x+6) = 0
x1 = -6
x2 = 8
y1 = 540 = (-6)³ -3*(-6)² - 144*(-6) = -216 -108 + 864 = -324 + 864 = 540
y2 = -832 = 8³ -3*8² -144*8 = 8*64 - 3*64 - 144*8 = 5*8*8 - 144*8 =
= 8*(40-144) = 8*(-104) = -800 -32= -832
3)
f(2) = 4-16+15 = 3
f(5) = 25 -40 +15 =0
f'(x) = 2x-8
f'(x) = 0 при х = 4
f(4) = 16 - 32 +15 = -1
из f(2)=3, f(4)= -1, f(5)=0 выбираем минимум и максимум
минимум f(4)= -1
максимум f(2)=3
прим.: на втором таки уткнулся. противно его считать в голове. по быстрому там тупо решается квадратное уравнение через дискриминант на листике
1)
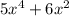
2)
функция - не монотонная
экстремумы: (-6; 540), (8; -832)
3)
минимум f(4)= -1
максимум f(2)=3
Пошаговое объяснение:
1)
просто диференцируем по частям
2)
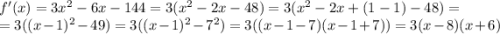
это производная исходной функции
как бы тут уже видно, что производная:
квадратичная парабола,
роги вверх,
знак меняет (а это значит, что исходная функция - не монотонная) в точках: x1 = -6; x2 = 8. это и будут точки экстремумов
минимум и максимум производной нас не интересуют
Решаем уравнение
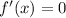
3(x-8)(x+6) = 0
x1 = -6
x2 = 8
y1 = 540 = (-6)³ -3*(-6)² - 144*(-6) = -216 -108 + 864 = -324 + 864 = 540
y2 = -832 = 8³ -3*8² -144*8 = 8*64 - 3*64 - 144*8 = 5*8*8 - 144*8 =
= 8*(40-144) = 8*(-104) = -800 -32= -832
3)
f(2) = 4-16+15 = 3
f(5) = 25 -40 +15 =0
f'(x) = 2x-8
f'(x) = 0 при х = 4
f(4) = 16 - 32 +15 = -1
из f(2)=3, f(4)= -1, f(5)=0 выбираем минимум и максимум
минимум f(4)= -1
максимум f(2)=3
прим.: на втором таки уткнулся. противно его считать в голове. по быстрому там тупо решается квадратное уравнение через дискриминант на листике
1)3.72х + 0.13х = 6.16; х=6.16/(3.72+0.13);х=6.16/3.85; х=1.6
2)4.7х - 1.2х + 3.7 = 8,6; х=(8.6-3.7)/3.5;х=4.9/3.5; х=1.4
3)4.5(х-2.9) = 1,35; х-2.9=1.35/4.5;х=2.9+0.3; х=3.2
4) (2х - 7) : 0.02 = 100; 2х - 7=0,02 *100; 2х=7+2; х=9/2; х=4.5