1)2х•3y=6ху
2)4•5•8v=160v
3) 6(7+x)=42+6x
3) 2c+6c-5c=3c
4)5f+7b-2f+6b=3f+13b
5)9x-x-x=7x
6)6a+67+4a+37=10a+104
7)34x+12y+9-4x+65y+15=30x+77y+24
8)2(2x+4y-6a+8)=4x+8y-12a+16
9)6(16x+4s)+10(4x-2s)=96x+24s+40x-20s=146x+4s
10)56x(2x+3y)=112x^2+168xy
11)12(3a+5b+7) +5(4a-2b+9)=36a+60b+84+20a-20b+45=56a+40b+129
12)3ab+4ab+76=7ab+76
13)x•y•7•f•18=126xyf
14(9v+3p-8k)•7=63v+21p-56k
15)a+a=2a
16)b+b+b-3b=0
17)(4x+6y)•5+(5x-2y)•10=20x+30y+50x-20y=70x+10y=10(7x+y)
18)23(3x+4) +56=69x+92+56=69x+159
19)6f+10b-(5f+2b)=6f+10b-5f-2b=f+8b
20) (6a+3b)-2a=6a+3b-2a=4a+3b
21)6x-(2y-4x)=6x-2y+4x=10x-2y=2(5x-y)
22)65x•2•4=520x
23)34-(2x-5)=34-2x+5=39-2x
24) 58-(53d+12)=58-53d-12=46-53d
25)-2(3х+4у-5а)-6(-2х-6у+9а)=-6x-8y+10a-12x+36y-54a=16x-28y+44a
26)-(5a-6d+7c)-7(3a+5d-11c)=-5a+6d-7c-21a-35d+77c=26a+29d-56c
Пошаговое объяснение:
Пошаговое объяснение:
y=1/3x³ -7x²+38x-1=-2
-Можно получить, график, и то что я могу сделать это (-1) перенести после равно.
Тоесть получается:
у=1/3х³-7х²+38х=-2+1
у=1/3х³-7х²+38х=-1
(Это первый вариант, но он как таковой не подходит)
поэтому Мы равняем все к нулю.
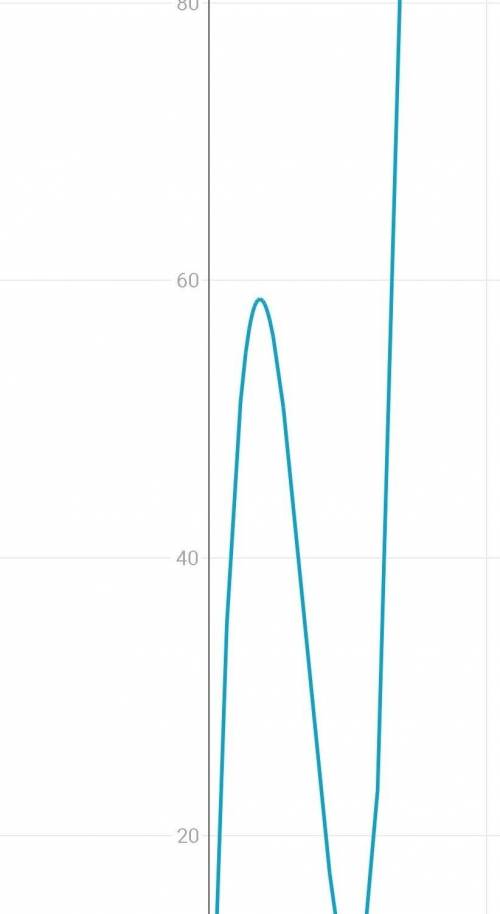
--Так как получается функция, линии,(Изогнутая гипербола)
То мы можем поставить разные значения "х".
у=1/3х³-7х²+38х-2-1=0
у=1/3х³-7х²+38х-3=0
•Например, берём область от -3 до 3
Х| -3 | -2 | -1 |0 | 1 | 2 | 3 |
У|-189|-109,6|-48,3|-3|28,3|47,6|57|
1)у(-3)=1/3×(-3)³-7×(-3)²+38×(-3)-3=-189
2)у(-2)=1/3×(-2)³-7×(-2)²+38×(-2)-3=-109,6
3)у(-1)=1/3×(-1)³-7×(-1)²+38×(-1)-3=-48,3
4)у(0)=1/3×(0)³-7×(0)²+38×(0)-3=-3
5)у(1)=1/3×(1)³-7×(1)²+38×(1)-3=28,3
6)у(2)=1/3×(2)³-7×(2)²+38×(2)-3=47,6
7)у(3)=1/3×(3)³-7×(3)²+38×(3)-3=57.
•Теперь, надо просто отметить на числовой оси точки, на оси Ох, и оси Оу. Точки имеют огромные числовые значения****
Удачи, тебе, солнце, во всём
Выразим через третий член и разность прогрессии все остальные члены:
Подставим получившиеся соотношения в уравнение:
Применяем формулы тангенса суммы и тангенса разности:
Из имеющегося соотношения для разности прогрессии выразим величины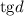 и
и 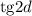 :
:
1)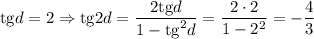
2)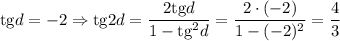
Первый случай: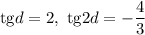
Замена: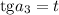
Числитель и знаменатель первой и последней дроби умножим на 3:
Складываем первые два слагаемых левой части уравнения:
Складываем последние два слагаемых левой части уравнения:
Складываем две получившиеся в предыдущих пунктах величины:
Тогда, уравнение примет вид:
Обратная замена: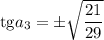
Находим требуемую величину:
Второй случай: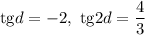
Заметим, что при подстановке этих значений в уравнение, получится такое же уравнение, как и в предыдущем случае с той лишь разницей, что первое и четвертое, а также второе и третье слагаемое будут поменяны местами. Значит, никаких новых результатов получено не будет.
ответ: 0.58