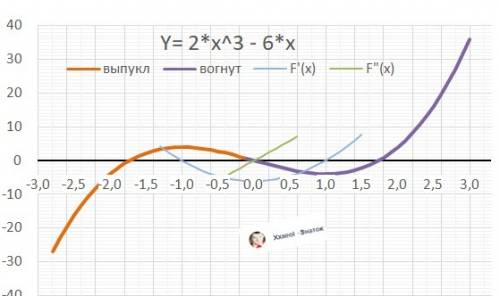
ДАНО: Y = 2*x³ - 6*x
ИССЛЕДОВАТЬ.
1. Область определения D(x) - Х∈(-∞;+∞) - непрерывная.
2. Пересечение с осью Х.
Y = 2*x*(x²-3) = 2*x(x-√3)*(x+√3) = 0
Y=0 при х₁ = - √3, Х₂ = 0, Х₃ = √3
Положительна - X∈(Х₁;Х₂)∪(Х₃;+∞), отрицательна - X∈(-∞;Х₁)∪(Х₂;Х₃).
3. Пересечение с осью У. У(0) = 0.
4. Поведение на бесконечности.limY(-∞) = - ∞ limY(+∞) = +∞
5. Исследование на чётность.Y(-x) = - 2*x³+6*x = - Y(x),
Функция нечётная.
6. Производная функции.Y'(x)= 6*x² -6 = 6*(x-1)(x+1).
Корни при Х₁= 1, Х₂ = -1 Схема знаков производной.
(-∞)__(>0)__(-1)___(<0)___(1)__(>0)_____(+∞)
7. Локальные экстремумы.
Максимум Ymax(-1)= 4 , минимум – Ymin(1) = - 4.
8. Интервалы возрастания и убывания.
Возрастает - Х∈[-∞; -1]∪[1;+∞), убывает = Х∈(-1; 1).
8. Вторая производная - Y"(x) = 12*x =0.
Корень производной - точка перегиба Y"(x)= 0.
9. Выпуклая “горка» Х∈(-∞; 0), Вогнутая – «ложка» Х∈(0; +∞).
10. График в приложении.
Пло́щадь — в узком смысле, площадь фигуры — численная характеристика, вводимая для определённого класса плоских геометрических фигур (исторически, для многоугольников, затем понятие было расширено на квадрируемыеПерейти к разделу «#Квадрируемые фигуры» фигуры) и обладающая свойствами площадиПерейти к разделу «#Свойства»[1]. Интуитивно, из этих свойств следует, что бо́льшая площадь фигуры соответствует её «большему размеру» (например, вырезанным из бумаги квадратом большей площади можно полностью закрыть меньший квадрат), a оценить площадь фигуры можно с наложения на её рисунок сетки из линий, образующих одинаковые квадратики (единицы площади) и подсчитав число квадратиков и их долей, попавших внутрь фигуры (на рисунке справа). В широком смысле понятие площади обобщается на k-мерные поверхности в n-мерном пространстве (евклидовом или римановом), в частности, на двумерную поверхность в трёхмерном пространствеПерейти к разделу «#Площадь поверхности».
Пошаговое объяснение: