Первая задача: Петерис должен будет вернуть через три года сумму в размере 4350 евро; вторая задача: у Иевы брать взаймы дешевле, потому что он просит вернуть на 10 евро больше, когда банк просит вернуть уже на 42 евро больше; третья задача: Ансису нужно будет вернуть через три года сумму в 4080 евро.
Пошаговое объяснение:
Первая задача: Петеритис взял ссуду в размере 3000 евро, сроком на 3 года. Ежегодная процентная ставка которой составляет 15%. Требуется найти ту сумму вместе с процентной ставкой, накопившейся за три года, которую ему потребуется вернуть.
Для начала найдем процентную ставку в 15% за один год от 3000 евро. Для этого можно составить пропорцию, где:
3000 евро - это 100%
x евро - это 115%
Такие пропорции решаются методом "крест накрест", мы перемножаем 3000 евро на 115% и делим на 100%. Тогда количество евро, которое ему потребуется вернуть через год будет равно:
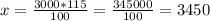евро - через год ему потребуется вернуть столько денег, откуда процентная ставка в 15% равна 450 евро. Тогда за три года эта сумма будет равняться уже 1350 евро. Поэтому по истечении трёх лет сумма выплаты составит 3000 евро которые он брал в долг и 1350 евро в качестве процентной ставки, в сумме 4350 евро.
Вторая задача: Иева одолжил Питэру 300 евро на шесть месяцев, но Иева просит вернуть на 10 евро больше. То есть через шесть месяцев Питэр должен будет вернуть 310 евро.
Банк же просит вернуть 14% сверх суммы в 300 евро. Найдем эти 14% аналогичной пропорцией:
300 евро - это 100%
x евро - это 114%
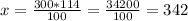евро - откуда процентная ставка в 14% равна 42 евро.
42 евро, которые потребуется отдать банку, более чем в 4 раза больше, чем потребуется отдать Иеве (10 евро), если одалживать деньги именно у неё. Поэтому у нее брать взаймы дешевле.
Третья задача: Ансис взял кредит в размере 3000 евро сроком на 3 года под процентную ставку равную 12% годовых. Данная задача аналогична первой. Где для начала находим те 15% за один год. Снова составляем пропорцию:
3000 евро - это 100%
x евро - 112%
Тогда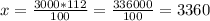 
евро Ансису потребуется вернуть через год. Откуда процентная ставка в 12% равна 360 евро за год. За три года эта сумма увеличится в три раза и будет равна 1080 евро.
Поэтому по истечении трех лет Ансису нужно будет вернуть 3000 евро, которые он брал в кредит и 1080 евро в качестве 12% ставки за три года. Поэтому в сумме получаем 4080 евро.
7.
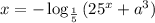
Пусть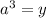
, количество корней от этого не изменится.
Рассмотрим функцию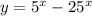
:
До точки экстремума функция возрастает, а после — убывает. Значит, это точка максимума. Максимальное значение функции равно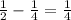
. Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
ответ:![(0; \frac{\sqrt[3]{2}}{2})](/tpl/images/0445/7312/80965.png)
8. При изменении размеров пирамиды соотношения между соответственными элементами не изменятся, поэтому примем для простоты вычислений сторону основания за 1.
Рассмотрим первую пирамиду:
Пусть SKM — сечение пирамиды SABCD, где K и M — середины BC и AD соответственно. Тогда в это сечение попадает окружность, вписанная в треугольник SKM и касающаяся KM в точке S' (проекция точки S), SK в точке K'. Пусть ∠SKS' = α, KO₁ — биссектриса, тогда:
Учитывая, что угол находится в первой четверти,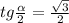
Рассмотрим вторую пирамиду:
Пусть S₁A₁C₁ — сечение пирамиды S₁A₁B₁C₁D₁. Это сечение содержит окружность, вписанную в треугольник S₁A₁C₁, касающуюся стороны A₁C₁ в точке S₁' (проекция точки S₁) и стороны S₁A₁ в точке A₁'. Пусть ∠S₁A₁S₁' = β, A₁O₂ — биссектриса. Тогда:
Решая аналогичное уравнение, получаем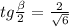
ответ: 4 : 3