1) 2⁴ = 16
Делители: 2⁰=1; 2¹=2; 2²=4; 2³=8 и 2⁴=16.
Всего 5.
2) 2³·3² = 8·9 = 72
Делители: 2⁰·3⁰=1; 2⁰·3¹=3; 2⁰·3²=9; 2¹·3⁰=2; 2¹·3¹=6; 2¹·3²=18; 2²·3⁰=4; 2²·3¹=12; 2²·3²=36; 2³·3⁰=8; 2³·3¹=24 и 2³·3²=72.
Всего 12.
3) 
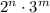
Представим делитель данного числа в виде произведения двух взаимно простых множителей: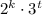 
, где k и t - целые числа, при этом 0≤k≤n и 0≤t≤m.
Множитель кратный двум можно выбрать А множитель кратный трём можно выбрать Значит, всего (n+1)·(m+1) делителей.
(По двум сторонам и углу между ними | сус)
2) Если сторона и прилежащие к ней углы одного треугольника равны стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны
(по стороне и прилежащей к ней двум углам | усу)
3) Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
(по трем сторонам | ссс)