при 
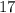и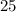 
– среднеарифметическое равно 
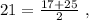и при этом 
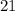на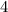 
меньше двадцати пяти и на 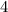больше семнадцати.
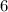монет и у них становится поровну, то они как раз и приходят к среднеарифметическому их начальных количеств монет. В итоге у Васи оказывается на 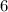монет меньше изначального, а у Пети на 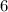монет больше изначального. А значит, вначале у Васи было на 
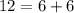монет больше, чем у Пети.
монет. Тогда у Пети 
монет.
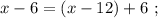
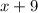монет, а у Пети-II будет 
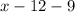монет. При этом у Пети-II монет в 
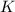раз меньше, т.е. если мы количество монет Пети-II мысленно увеличим в 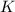раз, то их станет столько же, сколько и у Васи-II. На этом основании составим уравнение: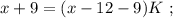
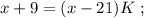
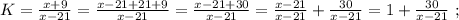
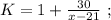
было целым, целой должен быть и результат деления в дроби, а чтобы 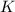было максимальным, частное от деления в дроби должно быть максимальным, а значит её знаменатель должен быть минимальным, целым, положительным числом, что возможно только, когда 
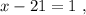откуда: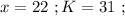
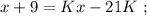
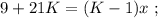
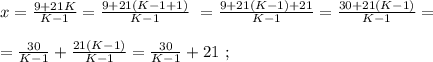
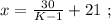
было целым, целой должен быть и результат деления в дроби. А максимальное значение знаменателя в такой дроби (при том, что частное от деления остаётся целым) составляет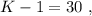 
откуда: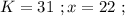
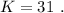
1) (x + y) * 4 = A.
2) (y + z) * 6 = A.
3) (x + z) * 12 = A.
Теперь надо решить систему уравнений. Ну, умножим первое уравнение на 3 и второе уравнение на 2. Получится такая система:
1) 12*(x+y)=3A.
2) 12*(y+z)=2A.
3) 12*(x+z)=A.
Недолго думая, сложим все уравнения и получим уравнение-следствие:
24*(x+y+z)=6A, или, сократив, 4*(x+y+z)=A. В принципе, ответ к задаче уже дан: 4 часа. Однако, сравнив это уравнение с первым, видим, что z=0. Кроме того, по условию задачи, убрать поле за 4 часа могут и первый со вторым. Таким образом, третий комбайн имеет нулевую мощность, не работает. Странный комбайн, обычно дают реальные задачи. Подставив в наши уравнения 2 и 3 вместо z ноль, получим y=2x, то есть второй комбайн в два раза мощнее первого. Проверить ответ можно подстановкой: мощность первого комбайна x, второго 2x, а третьего - ноль.