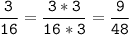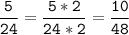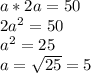 Это в том случае, если оба числа положительные, тогда меньшее равно 5, большее 5*2=10, а их произведение 5*10=50. Однако, если числа отрицательные, то получается следующая картина: Рассмотрим отрицательные числа. Пусть теперь b-наибольшее число из двух, следовательно наименьшее будет 2*b. Их произведение равно 50. Решим уравнение :
Это в том случае, если оба числа положительные, тогда меньшее равно 5, большее 5*2=10, а их произведение 5*10=50. Однако, если числа отрицательные, то получается следующая картина: Рассмотрим отрицательные числа. Пусть теперь b-наибольшее число из двух, следовательно наименьшее будет 2*b. Их произведение равно 50. Решим уравнение : 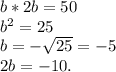 Такие образом, получаем два ответа: когда числа положительные и когда отрицательные. В первом случае (пол.) наим. число 5, когда же числа отр. наименьшее число -10.
Такие образом, получаем два ответа: когда числа положительные и когда отрицательные. В первом случае (пол.) наим. число 5, когда же числа отр. наименьшее число -10.
Чтобы найти НОД чисел нужно разложить их на простые множители и перемножить между собой общие множители (подчёркнуты).
Чтобы сократить дробь, нужно числитель и знаменатель разделить на НОД.
1) 24 = 2 * 2 * 2 * 3
60 = 2 * 2 * 3 * 5
НОД (24; 60) = 2 * 2 * 3 = 12

2) 45 = 3 * 3 * 5
105 = 3 * 5 * 7
НОД (45; 105) = 3 * 5 = 15
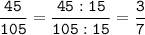
3) 39 = 3 * 13
130 = 2 * 5 * 13
НОД (39; 130) = 13
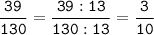
4) 64 = 2 * 2 * 2 * 2 * 2 * 2
144 = 2 * 2 * 2 * 2 * 3 * 3
НОД (64; 144) = 2 * 2 * 2 * 2 = 16
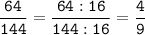
===========================================================
Чтобы найти НОК чисел, нужно разложить их на простые множители и к множителям бОльшего числа добавить недостающие множители (подчёркнуты) и перемножить их между собой.
Наименьшее общее кратное и будет наименьшим общим знаменателем.
1) 12 = 2 * 2 * 3
8 = 2 * 2 * 2
НОК (12; 8) = 2 * 2 * 3 * 2 = 24


2) 9 = 3 * 3
15 = 3 * 5
НОК (9; 15) = 3 * 5 * 3 = 45

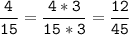
3) 25 = 5 * 5
15 = 3 * 5
НОК (25; 15) = 5 * 5 * 3 = 75
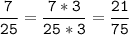
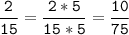
4) 16 = 2 * 2 * 2 * 2
24 = 2 * 2 * 2 * 3
НОК (16; 24) = 2 * 2 * 2 * 3 * 2 = 48