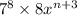
Нам дана пряма СО, перпендикулярна до площини або вісь проекції, а також дві точки S і А, які лежать за межами цієї площини. Ми хочемо знайти проекцію точки А на цю вісь.
Позначимо довжину ЅА як х і використаємо теорему Піфагора в трикутниках ЅАО та ОАВ, де В - проекція точки А на площину а.
Відстань від точки О до прямої ЅА дорівнює проекції відрізка ЅА на ось ОХ. Оскільки SO є перпендикуляром до цієї відрізка, довжина ЅО дорівнює
ОЅ² = ОА² + ЅА²
15² = ОВ² + (х + 3)²
Оскільки Об - проекція точки В на ось ОХ, або проекція точки А на площину а, ми можемо записати:
ОВ² = (х + 3)² - х² = 6х + 9
Підставляючи це значення в формулу, пов'язану з теоремою Піфагора, ми отримуємо:
15² = 6х + 9 + (х + 3)²
Розв'язуючи це рівняння, ми отримаємо:
225 = 7х² + 42х + 72
7х² + 42х - 153 = 0
Після розв'язання квадратного рівняння ми отримуємо:
х = 3 або х = -9
Оскільки х не може бути від'ємним числом, ми отримуємо:
х = 3 см
Таким чином, проекція відрізка ЅА на проекційну ось дорівнює х + 3 = 6 см.
Пошаговое объяснение:
Для вирішення цієї задачі необхідно використовувати формулу для обчислення площі прямокутника.
Площа прямокутника дорівнює добутку його довжини на ширину. В даному випадку, заасфальтована частина доріжки являє собою прямокутник, довжина якого дорівнює довжині всієї доріжки, а ширина - довжині ділянки, який заасфальтували.
Таким чином, площу заасфальтованої ділянки можна обчислити, помноживши довжину всієї доріжки на довжину ділянки, яка була заасфальтована:
S = L * L1
де S - площа заасфальтованої ділянки, L-довжина всієї доріжки, L1-довжина ділянки, яка була заасфальтована.
Підставляючи значення з умови, отримаємо:
210 * x = S
Так як довжина заасфальтованої частини дорівнює ширині заасфальтованого прямокутника, то її довжина дорівнює:
L2 = S / L1 = (210 x) / x = 210 метрів
Відповідь: довжина заасфальтованої частини доріжки становить 210 метрів.
16.
Пошаговое объяснение:
В данном одночлене одна переменная. Поэтому степень одночлена равна n + 3.
По условию
n + 3 = 19
n = 19 - 3
n = 16
ответ: 16.
(Степень одночлена стандартного вида – это сумма показателей степеней всех переменных, входящих в его запись).