Математика: Разделите с остатком и проверьте: 1234: 10=? 2345: 10=? 34567: 100=?

Можно найти несколько пределов данной числовой последовательности. Для этого нужно посмотреть, что произойдет с ней при стремлении к бесконечности с разными знаками, и в опасных точках. Опасные точки сразу видны, это: 1) - знаменатель обращается в 0. 2) - по обычаю проверяется эта точка. Эта числовая последовательность может быть сведена ко второму замечательному пределу для нахождения пределов: (при →∞) Выделяем целую часть в дроби: Используем свойство 2-го замечательного предела, но добавляем...

Разделите с остатком и проверьте: 1234: 10=? 2345: 10=? 34567: 100=?

👇

Увидеть ответ

Ответ:

ilonasuper

17.04.2022

1234:10=123 (4 остаток). Проверка: 123х10+4=1234.

2345:10=234 (5 остаток). Проверка: 234х10+5=2345.

34567:100=345 (67 остаток). Проверка: 345х100+67=34567.

4,7(97 оценок)

Ответ:

Александра030307

17.04.2022

1234:10 = 1230 (остаток 4)
2345:10= 2340 (остаток 5)
34567:100= 34500 (остаток 67)

4,7(67 оценок)

Открыть все ответы

Ответ:

kthjxrfqqq

17.04.2022

10 - 11 классы Геометрия 21 балл

В правильной четырехугольной пирамиде сторона основания равна 6 см, а угол наклона боковой грани к плоскости основания равен 60 градусов. Найдите боковое ребро пирамиды

По больше объяснений Следить Отметить нарушение Missvolodya 18.03.2011

ответ

Проверено экспертом

ответ дан

KuOV

Пирамида правильная, значит в основании квадрат, боковые грани - равные равнобедренные треугольники, высота прецируется в точку пересечения диагоналей квадрата.

Пусть Н - середина CD. Тогда SH - медиана и высота равнобедренного треугольника SCD, ОН - медиана и высота равнобедренного треугольника OCD.

SH⊥CD, OH⊥CD, ⇒∠SHO = 60° - линейный угол двугранного угла между боковой гранью и основанием.

ОН = AD/2 = 6/2 = 3 cм как средняя линия ΔACD.

ΔSOH: ∠SOH = 90°, cos∠SHO = OH/SH

SH = OH / cos∠SHO = 3 / (1/2) = 6 см

ΔSHC: ∠SHC = 90°, SH = 6 см, HС = 3 см, по теореме Пифагора:

SC = √(SH²+ HC²) = √(36 + 9) = √45 = 3√5 см

4,4(8 оценок)

Ответ:

LoveSmile78900987

17.04.2022

Можно найти несколько пределов данной числовой последовательности. Для этого нужно посмотреть, что произойдет с ней при стремлении к бесконечности с разными знаками, и в "опасных" точках.

"Опасные" точки сразу видны, это:
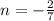1) $n=- \frac{2}{7}$ - знаменатель обращается в 0.
2) n=0

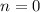- по обычаю проверяется эта точка.

Эта числовая последовательность может быть сведена ко второму замечательному пределу для нахождения пределов:
$lim (1+ \frac{1}{x})^x=e$ (при

→∞)

Выделяем целую часть в дроби:

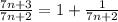
$\frac{7n+3}{7n+2 } = 1 + \frac{1}{7n+2 }$

Используем свойство 2-го замечательного предела, но добавляем степени:

$lim (1 + \frac{1}{7n+2 })^{3n-4}$

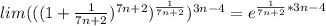$lim (((1 + \frac{1}{7n+2 })^{7n+2})^{ \frac{1}{7n+2}})^{3n-4} = e^{\frac{1}{7n+2} * 3n-4}$ (при

→∞)

То есть мы степень не меняли: домножили и разделили.

Посчитаем, что получилось:

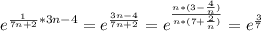$e^{\frac{1}{7n+2} * 3n-4} = e^{ \frac{3n-4}{7n+2}} = e^{ \frac{n*(3-\frac{4}{n}) }{n*(7+\frac{2}{n})} } = e^{ \frac{3}{7} }$ (при

→∞)

Итак:
1)

→+∞ предел равен $e^{ \frac{3}{7} }$
2)

→-∞ предел равен $e^{ \frac{3}{7} }$

3)

→0 предел равен:
$lim ( \frac{7n+3}{7n+2})^{3n-4} = (\frac{3}{2})^{-4} = (\frac{2}{3})^{4} = \frac{16}{81}$

4)

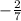
→ $- \frac{2}{7}$
По правило Лопиталя имеем: 0 (не расписывал, поскольку это очень много и неважно в данном случае, нас это не интересует).

Мы видим, что при стремлении к бесконечности с разными знаками, мы имеем конечное число. В "опасных" точках, скачков нет.

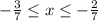Используя свойства показательной функции, находим, что график делает скачок в некотором интервале (основание должно быть неотрицательным числом, если же взять число из интервала $- \frac{3}{7} \leq x \leq - \frac{2}{7}$ - мы получаем отрицательное основание).

Можно говорить, что данная числовая последовательность является неограниченной (из-за этого интервала).

Если же этого не учитывать, то данная числовая последовательность является ограниченной (это очень грубо).

Найдите предел числовой последовательности. укажите, является ли заданная числовая последовательност