1) 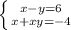
x-y=6
x=6+y 6+у+6у+у^2=-4
у^2+7у+10=0
у1= -2
у2= 5
х1= 6+2= 8
х2= 6-5 = 1
ответ: (8; -2) ; (1;5)
5) 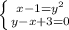
у-х+3=0
-х=-3-у
х= 3-у 3-у-1=y^2
-у^2-у+2=0
y^2+y-2=0
y1= 1
y2= -2
x1= 3-1 = 2
x2= 3+2 = 5
ответ: (2;1) ; (5;-2)
3) 
x-y=1
-y=1-x
y= x-1 x^2-2x+2-26=0
x^2-2x-24=0
x1= 6
x2= -4
y1= 6-1 = 5
y2= -4-1 = -1
ответ: (6;5) ; (-4; -1)
Пошаговое объяснение:
1) Проверяем правильность утверждения при малых n.
n=1: 1=1² - верно
n=2: 1+3=2² - верно
n=3: 1+3+5=3² - верно
2) Предположим, что утверждение верно для n=k.
Тогда справедливо равенство 1+3+5++(2k-1)=k².
3) Докажем, что утверждение верно и для n=k+1.
Слева и справа добавим по 2(k+1)-1:
Получим 1+3+5++(2k-1)+(2(k+1)-1)=k²+2(k+1)-1
Преобразуем правую часть.
k²+2(k+1)-1=k²+2k+1=(k+1)².
Таким образом, из того, что 1+3+5++(2k-1)=k², следует то, что
1+3+5++(2k-1)+(2(k+1)-1)=(k+1)² - верно для n=k+1.
....................