Математика: Сократите с полным объяснением ❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️

Сократите с полным объяснением ❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️

👇

Увидеть ответ

Ответ:

DAYN777DEBIL

29.06.2022

Пошаговое объяснение:

Сократите с полным объяснением ❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️❤️

4,5(57 оценок)

Открыть все ответы

Ответ:

никита16l

29.06.2022

$a \in( -3; - 1) \cup(1;3)$

Пошаговое объяснение:

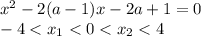
$x^2-2 (a-1)x-2a+1=0\\-4$

$x^2-2 (a-1)x-2a+1=0 \\ x^2 + 2 (1 - a)x + (1-2a)=0 \\$

Определим корни заданного квадр. уравнения:

Корни вычисляются по общей формуле:

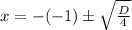
$x =-(-1) \pm\sqrt{\tfrac{D}{4}}$

Отдельно для х1 и х2:

$x_1= 1-\sqrt{\tfrac{D}{4}} \\ x_2 =1 + \sqrt{\tfrac{D}{4}}$

где D/4 - дискриминант для четного коэффициента при х:

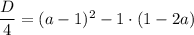
$\dfrac{D}{4}=(a-1)^2-1 \cdot(1 - 2a) \\$

Вычислим D/4

$\dfrac{D}{4}=a^{2} -2a + 1-1 + 2a = {a}^{2} \\ \dfrac{D}{4} \geqslant 0 \: \forall \: a \: \in \R$

т.е. хотя бы один корень есть для любого значения а

Однако, по условию требуется 2 корня, следовательно, появляются ограничения на а:

$\dfrac{D}{4} 0 < = {a}^{2} 0 < = \\ < = |a| 0 = a \neq0 \\$

Теперь определим х1 и х2:

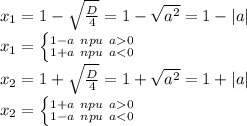
$x_1= 1-\sqrt{\tfrac{D}{4}} = 1 - \sqrt{ {a}^{2} } = 1 - |a| \\ x_1= \begin{cases} \large{^{1 - a\: \: npu \: \: a 0} _{1 + a\: \: npu \: \: a < 0}} \end{cases}\\ x_2 =1 + \sqrt{\tfrac{D}{4}} = 1 + \sqrt{ {a}^{2} } = 1 + |a| \\ x_2= \begin{cases} \large{^{1 + a\: \: npu \: \: a 0} _{1 - a\: \: npu \: \: a < 0}} \end{cases}\\$

Далее предлагаю рассмотреть отдельно варианты для положительных и для отрицательных значений а:

1) При а> 0 корни уравнения будут:

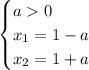
$\begin{cases}a 0 \\ x_1={1 - a}\: \\ x_2=1 + a\: \end{cases}$

из условия:

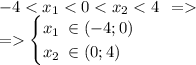
$- 4 < x_1 < 0 < x_2 < 4 \: \: = \\ = \begin{cases} x_1 \: \in( - 4; 0) \\ x_2 \: \in(0; 4)\end{cases}$

Обьединим:

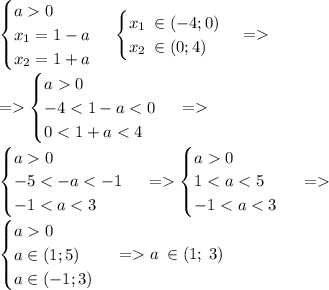
$\begin{cases}a 0 \\ x_1={1 - a}\: \\ x_2=1 + a\: \end{cases} \begin{cases} x_1 \: \in( - 4; 0) \\ x_2 \: \in(0; 4)\end{cases} = \\ = \begin{cases}a 0 \\ - 4 < {1 - a} < 0\: \\ 0 < 1 + a < 4\: \end{cases} = \\ \begin{cases}a 0 \\ - 5 < { - a} < - 1\: \\ - 1 < a < 3\: \end{cases} = \begin{cases}a 0 \\ 1< {a} < 5\: \\ - 1 < a < 3\: \end{cases} = \\ \begin{cases}a 0 \\ a \in(1;5)\: \\ a \in( - 1;3)\: \end{cases} = a \: \in( 1; \: 3) \\$

2)Для значений а < 0:

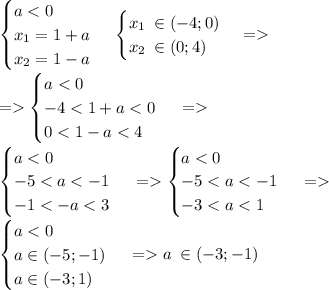
$\begin{cases}a < 0 \\ x_1={1 + a}\: \\ x_2=1 - a\: \end{cases} \begin{cases} x_1 \: \in( - 4; 0) \\ x_2 \: \in(0; 4)\end{cases} = \\ = \begin{cases}a < 0 \\ - 4 < {1 + a} < 0\: \\ 0 < 1 - a < 4\: \end{cases} = \\ \begin{cases}a < 0 \\ - 5 < { a} < - 1\: \\ - 1 < - a < 3\: \end{cases} = \begin{cases}a < 0 \\ - 5< {a} < - 1\: \\ - 3 < a < 1\: \end{cases} = \\ \begin{cases}a < 0 \\ a \in( - 5; - 1)\: \\ a \in( -3;1)\: \end{cases} = a \: \in( - 3; - 1) \\$