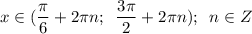Число 9841 выбрали не зря! Дальше я буду писать про каждый ящик отдельно. 1) Орехов x, пряников 9841, разность x-9841. 2) Орехов x+x-9841=2x-9841. Пряников 9841-(x-9841)=2*9841-x Разность 2x-9841-(2*9841-x)=3x-3*9841 Во 2 ящике орехов на столько больше, на сколько в 1 ящике орехов больше, чем пряников, то есть на разность. А пряников во 2 ящике на столько же меньше, чем в 1 ящике. Дальше всё тоже самое. 3) Орехов 2x-9841+3x-3*9841=5x-4*9841 Пряников 2*9841-x-(3x-3*9841)=5*9841-4x Разность 5x-4*9841-(5*9841-4x)=9x-9*9841 Дальше я не буду утомлять вас вычислениями, а просто напишу результаты. Кстати, в разностях коэффициенты всегда степени 3. 4) Орехов 14x-13*9841 Пряников 14*9841-13x Разность 27x-27*9841 5) Орехов 41x-40*9841 Пряников 41*9841-40x Разность 81x-81*9841 6) Орехов 122x-121*9841 Пряников 122*9841-121x Разность 243x-243*9841 7) Орехов 365x-364*9841 Пряников 365*9841-364x Разность 729x-729*9841 8) Орехов 1094x-1093*9841 Пряников 1094*9841-1093x Разность 2187x-2187*9841 9) Орехов 3281x-3280*9841 Пряников 3281*9841-3280x Разность 6561x-6561*9841 10) Орехов 9842x-9841*9841 Пряников 9842*9841-9841x Разность 19683x-19683*9841 По условию в 10 ящике пряников не было вообще. 9842x*9841-9841x = 0 9841*(9842-x) = 0 x = 9842 орехов было в 1 ящике.
Заготовленные шишки сосны, ели и лиственницы до момента переработки нужно хранить в деревянных амбарах и через каждые 2—3 недели перемешивать, чтобы не портились. высота слоя шишек не должна быть больше 1 м. извлеченные сухие семена выдерживают довольно высокую температуру (70° и более) без понижения всхожести, но семена влажные, находящиеся в шишках, при высоких температурах теряют всхожесть. особенно опасной для семян является не столько высокая температура, сколько высокая температура, соединенная с большой их влажностью. поэтому чрезвычайно важно, чтобы сушка шишек в шишкосушилынях сопровождалась хорошей вентиляцией.
График функции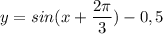 получается сдвигом графика
получается сдвигом графика 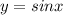 вдоль оси OX на
вдоль оси OX на 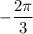 единиц и вдоль оси OY на -0,5 единиц.
единиц и вдоль оси OY на -0,5 единиц.
Свойства функции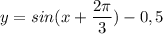 .
.
1) Область определения функции x ∈ (-∞; +∞).
2) Область значений функции y ∈ [-1,5; 0,5].
3) Периодичность. Функция периодическая с периодом T = 2π.
4) Четность функции не определенная (не является четной, не является нечетной).
5) Нули функции.
y = 0 при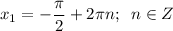 и
и 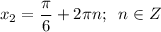
Решение
6) а) Наибольшее значение функции y = 0,5 при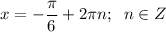
б) Наименьшее значение функции y = -1,5 при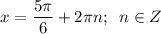
7) а) Функция убывает при![\displaystyle x \in[ -\frac{\pi }{6}+2\pi n ; \;\;\frac{5\pi }{6}+2\pi n] \;\;n \in Z](/tpl/images/1400/9661/4a1c3.png)
б) Функция возрастает при![\displaystyle x \in[ -\frac{7\pi }{6}+2\pi n ; \;\;-\frac{\pi }{6}+2\pi n] \;\;n \in Z](/tpl/images/1400/9661/c1e47.png)
8) Промежутки знакопостоянства
y > 0 при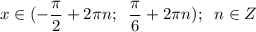
y < 0 при