Слово "CLEVERSLAND" состоит из 11 букв причем в нем содержатся 2-е буквы "E" каждый день он пишет по три буквы ; то тогда за 104 дня он напишет 104*3=312 букв Теперь найдем кол-во полных слов "CLEVERSLAND" разделив 312 на 11 то есть 312:11=28(ост 4 значит что пишем первый 4-е буквы из этого слова ) значит у нас выйдет так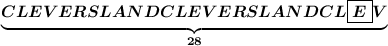 
Мы знаем что в одном слове CLEVERSLAND 2-е буквы то тогда букв "Е" 28*2=56 ; но в последних четырех буквах есть одна буква "E" ; и поэтому 56+1=57 букв "Е" ответ: В его записи буква "Е" будет встречаться 57 раз
Пошаговое объяснение:
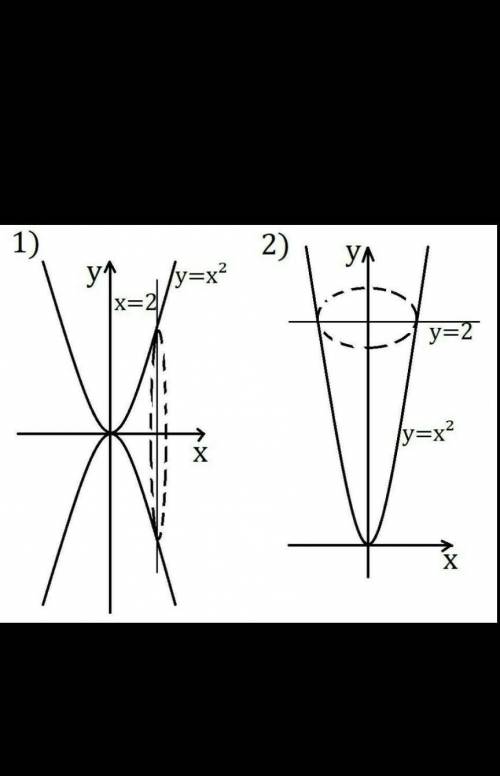
Объём тела, полученного при вращении вокруг оси Ox фигуры, ограниченной линиями y=x², x=0, x=2, равен:
\begin{gathered}\tt \displaystyle V=\pi \int\limits^2 _0 y^2 \; dx=\pi \int\limits^2 _0 x^4 \; dx=\pi \cdot \begin{pmatrix}\frac{x^5}5\end{pmatrix} \begin{vmatrix}\\ \\ \end{matrix} ^2 _0 =\\ \\ \\ =\pi \begin{pmatrix}\frac{2^5}5 -\frac{0^5}5\end{pmatrix} =\frac{32}5 \pi =6,\! 4\, \pi\end{gathered}
ответ: 6,4π.
2)
При x = -2, y = (-2)² = 4.
При x = 2, y = 2² = 4.
Надо найти объём тела, полученного при вращении вокруг оси Oy фигуры, ограниченной линиями y=x², y=4. \tt \displaystyle y=x^2 \rightarrow y_min =0y=x
2
→y
m
in=0
\begin{gathered}\tt \displaystyle V=\pi \int\limits^4 _0 x^2 \; dy=\pi \int\limits^4 _0 y \; dy=\pi \cdot \begin{pmatrix}\frac{y^2}2\end{pmatrix} \begin{vmatrix}\\ \\ \end{matrix} ^4 _0 =\\ \\ \\ =\pi \begin{pmatrix}\frac{4^2}2 -\frac{0^2}2\end{pmatrix} =8\pi \end{gathered}
ответ: 8π.
1+
2-
3+
4-
5+
Пошаговое объяснение:
Я не уверена что правильно