
1. в ящике 120 кг пшена. после того как из ящика отсыпали пшено в мешок, в ящике осталось 65% всего пшена. сколько кг пшена вошло в мешок?
решение: 120*0,65=78кг осталось в мешке
120-78=42 кг пшена вошло в мешок
ответ: 42 кг
2. в роще 700 берёз и 300 сосен. сколько поцентов всех деревьев составляют сосны?
решение: всего в роще 1000 деревьев
(300/1000)*100=30 % всех деревьев
ответ: 30 %
3. СО СКЛАДА ВЫГРУЗИЛИ 244,8 Т УГЛЯ, ПОСЛЕ ЧЕГО НА СКЛАДЕ ОСТАЛОСЬ 55% УГЛЯ. СКОЛКО ТОНН УГЛЯ БЫЛО НА СКЛАДЕ?
решение: 244,8 т = 45%
х = 100 %
х=(244,8*100)/45 = 544 т
ответ: 544 т
4. Товар стоил 4800 рублей.Перед праздниками его цена снизилась на 12%.Какова новая цена товара?
решение: 4800*0,88=4224 рублей
ответ: 4224 рублей
5.Решите уровнение: 1,7Х+21+3,1Х=57
решение: 4,8х=36
х=7,5
ответ: 7,5
6. В пакете лежали сливы. Сначала из него взяли 50% слив,а потом 40% остатка. После этого в пакете осталось 3 сливы.Сколько слив было в пакете первоночально?
решение: 1. 3 - 60%
х - 100%
х= 5 слив
2. 5 - 50%
х - 100%
х = 10 слив
ответ: 10 слив
1.Область определения функции: х ∈ R.
2. Нули функции. Точки пересечения графика функции с осью ОХ.
График функции пересекает ось X при f = 0
значит надо решить уравнение:
2 x + x^{3} - 3 x^{2} + 1 = 0.
Решение этого кубического уравнения даёт один действительный корень х = -0,32472.
3. Промежутки знакопостоянства функции:
y < 0, x ∈ (-∞; -0,32472),
y > 0, x ∈ (-0.32472; +∞).
4. Симметрия графика (чётность или нечётность функции).
Проверим функци чётна или нечётна с соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
2 x + x^{3} - 3 x^{2} + 1 = - x^{3} - 3 x^{2} - 2 x + 1. - Нет
2 x + x^{3} - 3 x^{2} + 1 = - -1 x^{3} - - 3 x^{2} - - 2 x - 1. - Нет
значит, функция не является ни чётной, ни нечётной.
5. Периодичность графика - нет периодичности.
6.Точки разрыва, поведение функции в окрестностях точек разрыва, вертикальные асимптоты.
Так как функция не содержит дробей и корней, то точек разрыва нет.
7. Интервалы монотонности функции, точки экстремумов, значения функции в точках экстремумов.
Производная функции y' = 3x² -6x + 2.
Корни уравнения 3x² -6x + 2 = 0 равны 1 +- (√3/3).
Максимум функции равен 1 + (2/(3√3)) при х = 1 - (√3/3),
минимум равен 1 - (2/(3√3)) при х = 1 + (√3/3).
8. Интервалы выпуклости, точки перегиба.
Вторая производная равна: y'' = 6х - 6 = 6(x - 1).
Поэтому точка перегиба одна: х = 1, у = 1.
9. Поведение функции в бесконечности. Наклонные (в частности, горизонтальные) асимптоты.
Наклонную асимптоту можно найти, подсчитав предел функции x^3 - 3*x^2 + 2*x + 1, делённой на x при x->+oo и x ->-oo
\lim_{x \to -\infty}\left(\frac{1}{x} \left(2 x + x^{3} - 3 x^{2} + 1\right)\right) = \infty.
Предел равен ∞, значит, наклонной асимптоты слева не существует.
\lim_{x \to \infty}\left(\frac{1}{x} \left(2 x + x^{3} - 3 x^{2} + 1\right)\right) = \infty.
Предел равен ∞, значит, наклонной асимптоты справа не существует.
Горизонтальные асимптоты найдём с пределов данной функции при x->+oo и x->-oo
\lim_{x \to -\infty}\left(2 x + x^{3} - 3 x^{2} + 1\right) = -\infty.
Предел равен -∞.
Значит, горизонтальной асимптоты слева не существует.
\lim_{x \to \infty}\left(2 x + x^{3} - 3 x^{2} + 1\right) = \infty.
Предел равен ∞, значит, горизонтальной асимптоты справа не существует.
10. Дополнительные точки, позволяющие более точно построить график.
y(x)=x3−3x2+2x+1y(x)=x3−3x2+2x+1Таблица точек:
x y-2.0 -23 -1.5 -12.1 -1.0 -5 -0.5 -0.9 0 1 0.5 1.4 1.0 1 1.5 0.6 2.0 1 2.5 2.9 3.0 7 3.5 14.1 4.0 25
11. Построение графика функции по проведенному исследованию - дан в приложении.
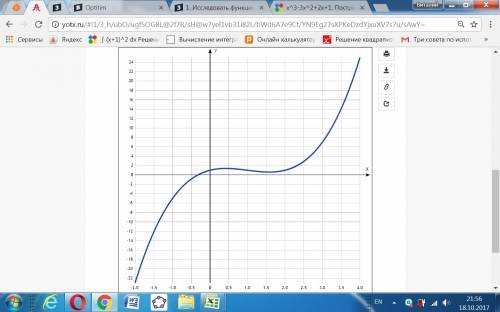
Пошаговое объяснение:
№ 66
18 девочек и 27 мальчиков
Чтоб найти НОД чисел 18 и 27 ,
18 = 2*3*3
27=3*3*3
НОД ( 18;27)= 3*3= 9
1) наибольшее число таких групп будет 9 , наименьшее 3
2) 18 : 9 = 2 девочки
27 : 9 = 3 мальчика в каждой группе
либо
18 : 3 = 6 девочек
27:3 = 9 мальчиков
в каждой группе
№67
12 тюльпанов и 35 нарциссов
НОК ( 12;35) = 1
12= 2*2*3
35= 5*7
наибольшее число букетов будет : 1 шт.