Рассмотрим случай, при котором квадратный корень из числа не извлекается нацело, и необходимо найти её приближённое значение. Воспользуемся методом извлечение квадратных корней столбиком. Допустим, необходимо найти приближённое значение √7. Чтобы извлечь квадратный корень из 7, нужно:
Разбить число, из которого мы извлекаем квадратный корень, на разряды справа налево по 2 цифры в каждом разряде. Если число содержит нечётное количество цифр, в данном случае "7" состоит из одной цифры. В этом случае нужно приписать слева от цифры ноль. Теперь нужно извлечь квадратный корень с недостатком из левого разряда по 2 цифры - это значит, что нужно извлечь квадратный корень из наибольшего целого числа, не превосходящего "7", из которого корень извлекается, извлекается корень из 4, √4 = 2, записываем "2" после знака "равно", а "4" приписываем под первым разрядом и вычитаем (7 - 4 = 3).Далее ставим разделительную черту, и справа от "3" записываем ещё две цифры следующего разряда, но у нас больше нет цифр, значит, дописываем мысленно после "7" запятую, а после запятой два нуля, и эти два нуля сносим к нашей цифре "3" ⇒ 300. Так как мы снесли эти два нуля после запятой, то нужно после "2" не забыть поставить запятую и продолжить извлечение корня.Для того чтобы продолжить вычисления, необходимо умножить "2" на 2 ⇒ "4" и записать слева от черты. После полученной "4" ставим звёздочку, под звёздочкой ещё одну звёздочку.Теперь надо подобрать, какую цифру нужно поставить вместо этой звёздочки так, чтобы произведение этого двузначного числа (4*) на однозначное (*) не превосходило бы "300", но было бы при этом максимальным. Возьмём 7, 47•7 = 329 > 300 - не подходит, берём 6, 46•6 = 276 < 300 - подходит (максимальное) и теперь вычитаем (300 - 276 = 24). То, что вместо звёздочки записали, это как раз будет следующая цифра в нашем корне.Дальше то же самое, сносим следующие две цифры следующего разряда, то есть ещё два нуля, получаем "2400". Умножаем число "26" на 2, не обращая внимание на запятую ⇒ "52", оставляем место для звёздочки. Вместо звёздочки подбираем такую цифру, чтобы " 52*•* " не превысило бы "2400", берём 4, 524•4 = 2096 - подходит (максимальное) и вычитаем (2400 - 2096 = 304). То, что вместо звёздочки записали, записываем в результат. Дальше то же самое, см. приложение. В итоге получаем приближённое значение, √7 ≈ 2,6457513 ≈ 2,64 ≈ 2,6, а насколько находить приближённое значение квадратного корня, это уже на ваше предпочтение.Вначале метод кажется очень сложным, но в ходе систематического её применения, можно легко извлекать квадратные корни столбиком. Метод работает и для чисел, из которых квадратный корень извлекается нацело и необходимо найти это извлечение (см. приложение). После прочтения "плана" можно задасться вопросом, почему ж мы в процессе извлечения корня умножали на 2 ? Если мы извлекали бы корень третьей степени, то умножали бы на 3, если пятой степени, на 5 и т.д. И вместо звёздочек можно ставить точки. Конечно, есть ещё один метод извлечения квадратных корней, легче, при формулы квадрата суммы, но этот метод стоит времени.

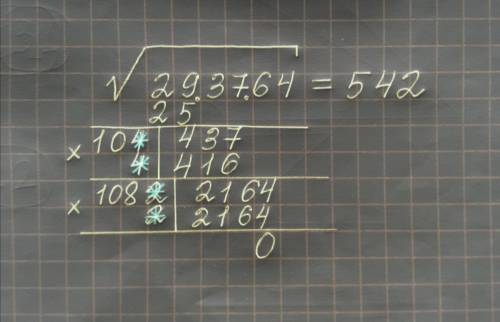
1. 3,34 + 28,7 = 32,04
2. 7 = 7/1; 14/2; 21/3; 28/4; 35/5 и т.д.
3. 1ч + 2ч = 3 ч - длится спектакль
4. 0,34 * 0,8 = 0,272
5. 20,4 : 0,8 = 25,5
6. 1 км = 1000 м 0,002 км * 1000 м = 2 м
7. S = a * a S = 11 * 11 = 121 (кв.см)
8. 3,784; 3,7801; 3,78
9. 3,46 * 10 + 23 = 346 + 23 = 369
10. Сумма смежных углов 180 градусов; 180 - 23 = 157 градусов второй угол
11. 22 : 55 * 100 = 40 человек в классе
12. S = 10 * (10 : 4) = 10 * 2,5 = 25 (кв.см)
13. 62 : 100 * 15 = 9,3 (кг) - продали; 62 - 9,3 = 52,7 (кг) - осталось продать
14. Прямой угол равен 90 градусов.
15. 8у = 24,1 - 5,7
8у = 18,4; у = 18,4 : 8; у = 2,3
16. 18,3 - 2,6 = 15,7 (км/ч) - собственная скорость лодки
15,7 - 2,6 = 13,1 (км/ч) - скорость лодки против течения реки
17. (20000 * 6) : 100 * 5 = 6000 (руб) - скидка
20000 * 6 - 6000 = 114000 (руб) - надо заплатить
18. х - один угол, 2х - второй
180 : (х + 2х) = 180 : 3х; х = 180 : 3 = 60 (градусов) - первый угол; 60 * 2 = 120 (градусов) - второй угол