"Центр тяжести тела
Подобно тому, как задача о вычислении центра тяжести плоской фигуры вычислялась с двойного интеграла, задача об отыскании центра тяжести тела решается аналогичным с тройного интеграла."
z0 = integral(z*dx*dy*dz) / integral(dx*dy*dz)
причем по z пределы интегрирования от 0 до 2/3, поскольку поверхность sqrt(x^2+y^2)=2 пересекает конус 3z=sqrt(x^2+y^2) как раз при z=2/3
integral(z*dx*dy*dz) = integral(z*(pi*2^2-pi*9*z^2)*dz) = pi* integral((4z-9*z^3)*dz) = pi*(4z^2/2-9z^4/4) от 0 до 2/3 = pi*(4(2/3)^2/2-9*(2/3)^4/4) = 1.3962634
integral(dx*dy*dz) = integral((pi*2^2-pi*9*z^2)*dz) = pi* integral((4-9*z^2)*dz) = pi*(4z-9z^3/3) от 0 до 2/3 = pi*(4*(2/3)-9*(2/3)^3/3) = 5.5850536
z0 = 1.3962634/5.5850536 = 0.25
30 шоколадок продал магазин за первый день.
Пошаговое объяснение:
Пусть в первый день каждая шоколадка стоила х тугриков, а всего продал магазин за этот день к шоколадок. Всего выручка в первый день составила хк - тугриков.
Во второй день каждая шоколадка стоила (х-2) тугрика, а всего магазин продал (к+10) шоколадок.
Выручка в этот день теперь составила (х-2)(к+10) тугриков.
На третий день продали (к-10) шоколадок, за (х+4) тугрика каждая шоколадка. Выручка в этот день составила (к-10)(х+4) тугриков.
Приравняем выручку первого и второго дня:
хк=(х-2)(к+10)
хк=хк-2к+10х-20
0=-2к+10х-20
Делим обе части на 2, получаем
0=-к+5х-10
Выразим х через к. Так как нам надо найти к.
Получаем:
5х=10+к
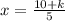 .
.
Приравняем выручку первого и третьего дня. Получим
(к-10)(х+4)=хк
хк-10х+4к-40=хк
-10х+4к-40=0.
Подставим значение х, выраженное через к, в последнее равенство, получим
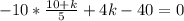
-2*(10+k)+4k-40=0
-20-2k+4k-40=0
-20-40+4k-2k=0
-60+2k=0
2k=60
k=60:2
k=30 шоколадок продали в первый день.
нешінші сынып нешінші есеп