В классе всего 12 + 18 = 30.
1) Вероятность выбрать первого мальчика равна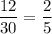 
. Одного человека мы выбрали уже, тогда в классе остается 11 мальчиков и 18 девочек. Вероятность выбрать второго мальчика равна 
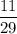. По теореме умножения, искомая вероятность: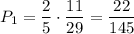 
2) Выбрать первую девочку можно с вероятностью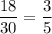 
. В классе остается 29 человек из них 17 девочек. Вероятность выбрать вторую девочку равна 
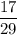. По теореме умножения, искомая вероятность: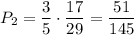 
3) Вероятность того, что среди двух выбранных человек окажутся девочка и мальчик, равна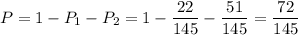 
ответ: 1) 22/145; 2) 51/145; 3) 72/145.
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Итак, монету бросают дважды. Если обозначить буквой Р выпадение решки (цифры), а буквой О - выпадение орла (герба), то все возможные выпадения можно записать так: РР, ОР, РО и ОО (соответствено, выпали две решки, орел потом решка, решка потом орел и два орла). Подсчитываем число этих комбинаций и получаем n=4. Теперь из них надо отобрать только те, что удовлетворяют условию "орел выпадет ровно один раз", это комбинации ОР и РО и их ровно m=2. Тогда искомая вероятность равна P=2/4=1/2=0.5.
Пошаговое объяснение:
5км/год ответ на этот вопрос