Для наглядности удобно провести некоторое соответствие с трехмерным пространством
Понятно что z(x,y) можно в нем изобразить как некоторую поверхность
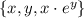
Точке (1,4) соответствует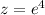 
, т.е. точка 
(*)
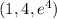Линию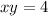 
удобнее записать как трехмерную кривую 
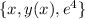, что будет пересекать поверхность z(x,y) при x=1
Запишем уравнение касательной к этой кривой в точке 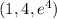, в качестве параметра берем переменную x
(#)
(вычисляется по аналогии с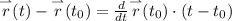 
)
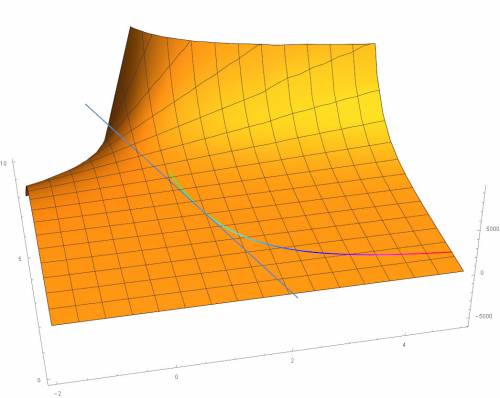
В прикрепленном файле нарисована поверхность, кривая и касательная.
Зная уравнение касательной, построим единичный вектор в направлении убывания x:
Пусть x=0, тогда из (#) получим точку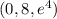 
Соотв. единичный вектор в направлении этой точки из (*) имеет вид
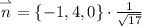
Понятно что z компонента никак не повлияет на значение производной по направлению, формально вектор можно записать как
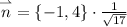
И, наконец, найдем искомую производную:
![grad[z(M_0)]\cdot\overset{\rightharpoonup }{n}=\left\{e^4,1 \cdot e^4\right\} \cdot \{-1,4\}\cdot\frac{1}{\sqrt{17} } = \frac{3 e^4}{\sqrt{17}} \approx 39.726](/tpl/images/0992/5590/2e9d7.png)
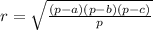
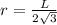
Пошаговое объяснение:
1)36,40,38,25,36,58,36
2)52,56,78,90,100,54,9