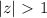 , то для возвращения к исходному числу 2018 придется выполнить умножение на число
, то для возвращения к исходному числу 2018 придется выполнить умножение на число 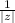 , которое будет являться дробным. Значит, другие числа по модулю не больше 1. Нулевых чисел также быть не может, так как в этом случае произведение будет равно 0.
, которое будет являться дробным. Значит, другие числа по модулю не больше 1. Нулевых чисел также быть не может, так как в этом случае произведение будет равно 0.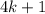 , где k - количество четверок (1, 1, -1, -1)
, где k - количество четверок (1, 1, -1, -1)
98502
Пошаговое объяснение:
9+8=17
8+5=13
5+0=5
0+2=2
2+9=11
все полученные числа являются простыми