8 с
Дано :
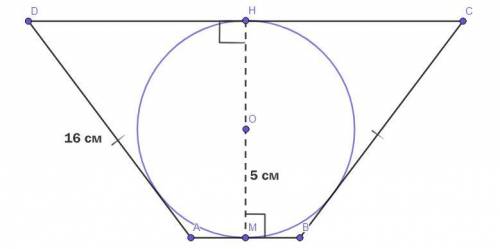
Четырёхугольник ABCD - равнобедренная трапеция (AB║DC, AD = BC).
Окружность с центром О - вписанная в равнобедренную трапецию окружность.
ОМ - радиус окружности = 5 см.
AD = BC = 16 см.
Найти :
S(ABCD) = ?
Если в четырёхугольник можно вписать окружность, то суммы противоположных сторон равны.
Следовательно -
AD + BC = AB + DC.
Но так как -
AD = BC = 16 см.
Поэтому -
AD + BC = 16 см + 16 см = 32 см
AB + DC = 32 см.
Радиус вписанной в трапецию окружности равен половине высоты.
На чертёже НМ - высота ABCD, следовательно -
НМ = 2*ОМ
НМ = 2*5 см
НМ = 10 см.
Площадь трапеции равна произведению полусуммы оснований и высоты.
То есть -
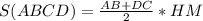
Теперь в формулу подставляем известные нам численные значения и считаем -
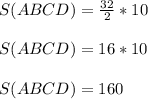
ответ : 160 (ед²).

"Найдите параллельные прямые и докажите,что они равны" - задание некорректно. Можно говорить о параллельных прямых и равных отрезках на них. Или о равных параллельных отрезках.
Решение задач опирается на равенство и сумму углов треугольников , теоремы о признаках параллельности двух прямых: Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.(№33) . Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны (№30).
№ 30
Рассмотрим Δ ABE и Δ CDF. BE = DF -- по условию; АС = ЕF --- по условию. AE = АС + СЕ; CF = ЕF+ СЕ. ⇒ АЕ = СF, так как состоят из равных частей. Внешние углы ∠BEF = ∠DFM по рисунку ⇒ равны и смежные внутренние углы этих треугольников. ⇒ Δ ABE = Δ CDF ( по 2 сторонам и углу между ними)
∠BEF = ∠DFM по условию, а это соответственные углы при прямых BE, DF и секущей АМ . ⇒ BE ║DF по признаку параллельности прямых, и отрезки BE и DF равны как соответствующие стороны равных треугольников
Прямые АВ и СD параллельны по признаку параллельности прямых , так как углы, образованные этими прямыми и секущей АМ равны как углы равных треугольников и эти углы ( ∠BАЕ и ∠DСF) являются соответственными. Отрезки АВ и СD равны как стороны равных треугольников
ответ: BE ║DF, BE =DF; АВ║СD, АВ =СD
№ 33
Рассмотрим Δ NRQ; RQ= NQ - по условию.⇒ Δ NRQ - равнобедренный с основанием NR. А углы при основании равнобедренного тр-ка равны. Так как сумма углов треугольника равна 180°, то ∠RNQ = (180°-30°)/2 = 75°
Рассмотрим Δ MNQ. ∠MQN = 30° + 45° = 75° -- по рисунку
∠NMQ = 180° - ∠RNQ - ∠MQN = 180° - 75° - 75° = 30°
∠KNM = ∠NMQ = 30°, а эти углы - внутренние накрест лежащие при прямых KN, MQ и секущей NM. ⇒ KN ║ MQ по признаку параллельности прямых
MN = МQ так как треугольник MNQ равнобедренный, это вытекает из равенства углов ∠RNQ и ∠MQN
В данной задаче можно найти только отрезок MQ, параллельный прямой KN, равных параллельных отрезков нет. Есть равные стороны в равнобедренных треугольниках (MN =MQ и RQ = NQ) , но они не параллельны.
ответ: KN ║ MQ.
8 секунд. Сам занимаюсь профессионально