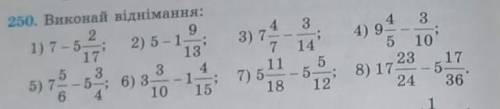
16с^2-25d^2 = (4c - 5d)(4c + 5d);
b^2-49a^2 = (b - 7a)(b + 7a);
144a^2b^2-289 = (12ab - 17)(12ab + 17);
c^2-100b^2 = (c - 10b)(c + 10b);
a^2b^2c^2-225 = (abc - 15)(abc + 15);
49a^2c^2-196 = 49•(a^2c^2 - 4) = 49•(ac - 2)(ac + 2);
x^8-y^8 = (x^4 - y^4)(x^4 + y^4) = (x^2 - y^2)(x^2 + y^2)(x^4 + y^4) = (x - y)(x + y)(x^2 + y^2)(x^4 + y^4);
256-81a^4 = (16 - 9a^2)(16 + 9a^2) = (4 - 3a)(4 + 3a)(16 + 9a^2);
625-c^4 = (25 - c^2)(25 + c^2) = (5 - c)(5 + c)(25 + c^2);
Если нет описки в условии, то
29d^2c^2x^2-196 = (√29dcx - 14)(√29dcx + 14);
144a^2-361b^2 = (12a - 19b)(12a + 19b);
36x^2y^2-121 = (6xy - 11)(6xy + 11);
m^2n^2-64 = (mn - 8)(mn + 8);
все просто для начала найдем количество способов при которых мы достаем 2 зеленых и 1 красный шарик. в вопросе между выбираемыми предметами стоит и соответственно умножаем сочетания зеленых и красных шариков
с₄²×с₅¹=4! /2! 2! × 5! /4! 1! =6×5=30 способов
теперь считаем сколько всего способов миша может выложить 3 шариками
с₉³=9! /3! 6! =84 способов
и наконец чтобы найти вероятность нужно просто найти отношение количества способов при которых выполняется условие и всего способов с 3 шариками
30/84=5/14=35,71%
Пошаговое объяснение:
1) 1целая 15/17
2) 3целых 4/13
3) 7целых 5/14
4) 9целых 1/2
5) 2целых 1/12
6) 2целых 1/30
7) 7/36
8) 12целых 35/72