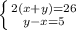
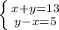
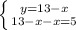
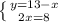
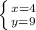ВС=у=9 смответ: 9 см.
Если три курицы за 3 дня снесли 3 яйца,
то те же три курицы за 1 день снесут 1 яйцо.
Тогда в 10 раз больше куриц (30) за 1 день снесут
в 10 раз больше яиц - 10 шт.
За 30 дней, таким образом, 30 куриц снесут в 30 раз больше,
то есть:
30*10 = 300 (шт.)
ответ: 30 куриц за 30 дней снесут 300 яиц.
Или так:
Исходное количество: куриц - 3; дней - 3; яиц - 3
При увеличении количества куриц в 10 раз и количества дней в 10 раз
количество яиц увеличится на: 10*10 = 100 раз.
Тогда:
3*100 = 300 (шт.)
ответ: 30 куриц за 30 дней снесут 300 яиц.
1. Находим и приравниваем нулю производную: y'=1+6*x=0, отсюда x=-1/6 - единственная критическая точка. Если x<-1/6, то y'<0, так что на промежутке (-∞;-1/6) функция убывает. Если же x>-1/6, то y'>0, так что на промежутке (-1/6;+∞) функция возрастает. ответ: функция убывает на промежутке (-∞;-1/6) и возрастает на промежутке (-1/6;+∞).
2. Находим первообразную F(x)=∫(x²-4)*dx=x³/3-4*x+C. Так как фигура лежит под осью ОХ, то искомая площадь S=-[F(2)-F(-2)]=F(-2)-F(2)=(-8/3+8)-(8/3-8)=16-16/3=32/3. ответ: S=32/3.
9) Из заданного соотношения х/у = 5/2 находим у = 2х/5.
Полупериметр прямоугольника равен 72/2 = 36.
С другой стороны он равен х + (х + у) = 2х + у = 2х + (2х/5).
Приравняем: 2х + (2х/5) = 36.
Приведём к общему знаменателю.
10х + 2х = 180 или 12х = 180, отсюда х = 180/12 = 15.
По свойству биссектрисы прямого угла имеем а = х.
ответ: а = 15.
10) Используем свойство высоты из прямого угла: АЕ/ВЕ = ВЕ/ЕС.
Так как ЕС = 3АЕ, то АЕ/ВЕ = ВЕ/3АЕ.
Отсюда ВЕ² = 3АЕ².
По Пифагору находим:
АВ = √(АЕ² + ВЕ²) = √(АЕ² + 3АЕ²) = √(4АЕ²) = 2АЕ.
АЕ = 10/4 = 2,5, тогда АВ = 2*2,5 = 5.
ответ: АВ = 5.