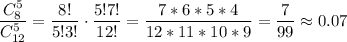Заданная система уравнений х^2 + у^2 = 2, х+|y| = a графически представляет собой 3 фигуры:
- окружность х^2 + у^2 = 2,
- прямую у = -х + а,
- прямую у = х - а.
Эти прямые взаимно перпендикулярны и чтобы было 2 решения, они должны касаться окружности каждая в одной точке.
Радиусы в точку касания параллельны прямым, но так как они идут из начала координат, то их уравнения у = х и у = -х.
Возьмём у = х и у = -х + а и приравняем: 2х = а, х =а/2, но и у = х = а/2.
Подставим ув уравнение окружности: (а²/4) + (а²/4) = 2, 2а² = 8,
а² = 8/2 = 4. Отсюда а = +-2.
ответ: наибольшее значение параметра а равно 2.
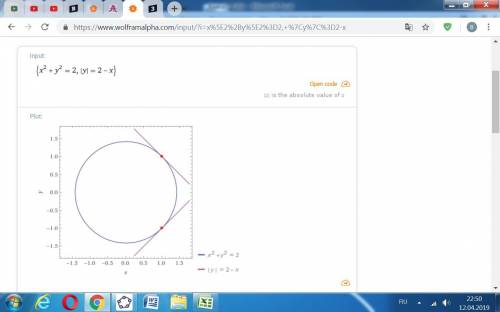
8/15
Пошаговое объяснение:
Для того , чтоб частное было целым , надо чтоб часы были больше минут .Рассмотрим возможные варианты :
8 :01 ; 9:01 ; 10:01 ; 11:01; 12:01 ;
частное будет
8 : 1=8
9 : 1=9
10 : 1=10
11 : 1=11
12 : 1=12
как видим, число целое
Если добавить 7 минут получим
8:08 ; 9:08 ; 10:08 ; 11:08 ; 12:08
Частное будет
8 : 8 = 1
9 : 8 = 1 1/8 - не целое
10 : 8 = 1 2/8 = 1 1/4 - не целое
11 : 8 = 1 3/8 - не целое
12 : 8 = 1 4/8 = 1 1/2 - не целое
Подходит только одно время :
8 :01 , через 7 мин будет 8 : 08 , еще через 7 мин будет 8 : 15
Частное будет : 8/15
Пошаговое объяснение:
Очевидно, т.к. черных шаров меньше 5, одного цвета шары могли оказаться лишь в случае, когда они все белые.
Число выбрать 5 из 8 белых шаров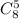 .
.
Всего вариантов достать 5 шаров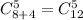
Искомая вероятность