Відповідь:
18 ОЛІВЦІВ.Покрокове роз'яснення:
Це завдання перевіряє вміння розв'язувати елементарні задачі з теми "Теорія ймовірностей".
1) Відомо, що формула ймовірності події має вигляд: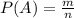 
, де A - подія; P(A) - ймовірність цієї події; n - кількість вcix можливих елементарних подій, а m - кількість елементарних подій, сприятливих А.
2) Думаємо так: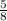 
- це ймовірність події витягнути одну ручку, нехай A - це ця подія, тоді 
.
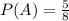3) Відомо, що олівців на 12 менше ніж ручок. Це означає, що якщо олівців є x (штук), то ручок тоді: x+12 (штук).
4) Захотівши один раз витягнути одну ручку, ви витягнете її, згідно умови, із олівців та всіх ручок, які є. Всього предметів у шухляді є лише ручки та олівці, тобто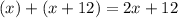 
- це кількість усіх предметів у шухляді.
5) Що таке ймовірність події витягнути одну ручку? - Це відношення кількості усіх подій "витягування ручки із шухляди" до "кількості усіх подій". Події "витягування ручки із шухляди" - це ті події, які сприяють появі події витягування одної ручки, тобто появі події, ймовірність якої дорівнює 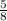. Тобто сприятливі події - це ті події, які задаються формулою x + 12
6) Знаючи, що ймовірність витягнути одну ручку дорівнює 5/8, тобто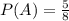 
; 
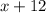- це сприятливі події до події A (m), а 
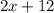- це кількість усіх подій (n), то складемо рівність опираючись на пункт 1 і знайдемо x, що і буде відповіддю на наше завдання:
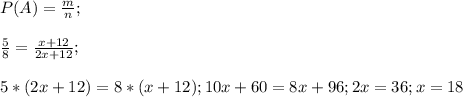
Тобто олівців у шухляді всього рівно 18.
(Гуманітарій - не оправдання)
Пошаговое объяснение:
Предположим, что утверждение задачи не верно. Обозначим сумму цифр числа n через S(n). Среди любых 39 последовательных натуральных чисел обязательно найдётся не менее трёх делящихся на 10; пусть a минимальное из них. При этом получаем, что среди данных 39 чисел также есть и a + 1,..., a + 29. Поскольку a делится на 10, то S(a + 1) = S(a) + 1, S(a + 2) = S(a) + 2,..., S(a + 9) = S(a) + 9. Поэтому среди чисел a, a + 1,..., a + 9 не встречается число, сумма цифр которого делится на 11, только если S(a) $ \equiv$ 1 mod 11. При этом если a + 10 не делится на 100, то S(a + 10) = S(a) + 1, а значит, среди чисел a + 10, a + 11,..., a + 19 найдётся такое, что сумма его цифр делится на 11. Получили противоречие. Осталось рассмотреть случай, когда a + 10 делится на 100. Но тогда заметим, что S(a + 20) = S(a + 10) + 1, а значит, аналогично первому случаю среди чисел a + 10, a + 11,..., a + 29 найдётся число, сумма цифр которого делится на 11. Опять получили противоречие, значит, утверждение задачи верно.